Sundaresan-Krishnaswamy Technique for Estimation of Process Parameters

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
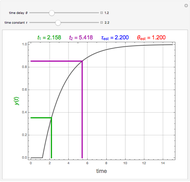
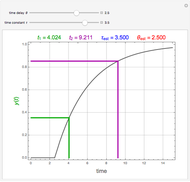
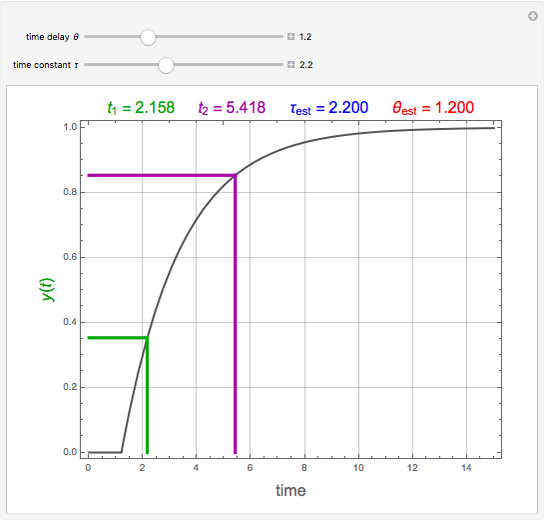
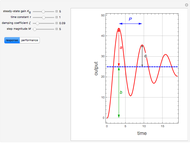
Consider a first-order plus delay model defined by the transfer function  , where
, where  ,
,  , and
, and  are the gain, time constant, and time delay, respectively. In order to find
are the gain, time constant, and time delay, respectively. In order to find  and
and  , Sundaresan and Krishnaswamy [1, 2] use the normalized response
, Sundaresan and Krishnaswamy [1, 2] use the normalized response  of the model to a step-forcing function:
of the model to a step-forcing function:  at two different times,
at two different times,  and
and  . These times are selected such that the normalized response reaches 35.3% at
. These times are selected such that the normalized response reaches 35.3% at  and 85.3% at
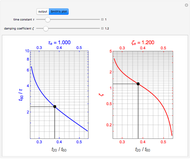
and 85.3% at  . The recipe gives the estimated values of the time constant and delay time by
. The recipe gives the estimated values of the time constant and delay time by  and
and  .
.
Contributed by: Housam Binous, Mohammad Mozahar Hossain, and Ahmed Bellagi (November 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] K. R. Sundaresan and P. R. Krishnaswamy, "Estimation of Time Delay Time Constant Parameters in Time, Frequency, and Laplace Domains," The Canadian Journal of Chemical Engineering, 56(2), 1978 pp. 257–262. doi:10.1002/cjce.5450560215.
[2] D. E. Seborg, T. F. Edgar, D. A. Mellichamp, and F. J. Doyle III, Process Dynamics and Control, 3rd ed., New York: Wiley, 2011.
Permanent Citation