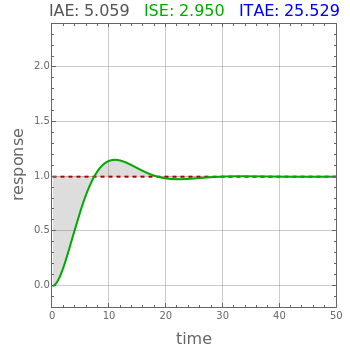
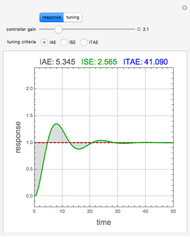
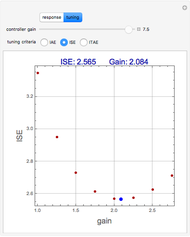
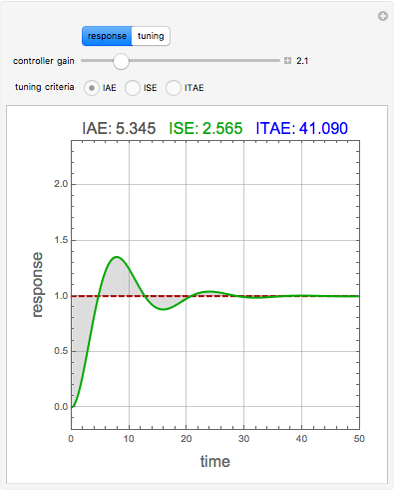
Integral Error Criteria for Controller Tuning
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
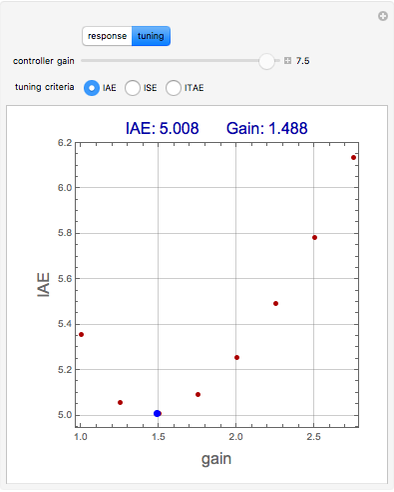
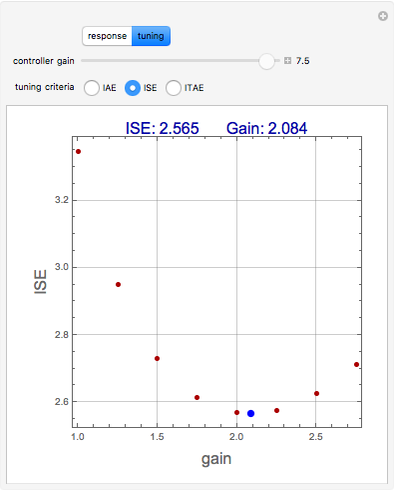
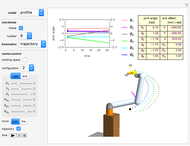
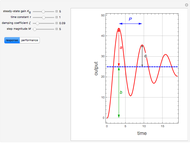
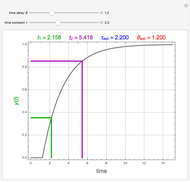
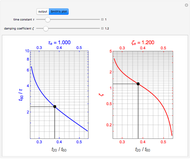
Consider the closed loop shown in Figure 10.8 in [1], where  ,
,  ,
,  ,
,  , and
, and  .
.
Contributed by: Housam Binous, Mohammad Mozahar Hossain, and Ahmed Bellagi (December 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] D. E. Seborg, T. F. Edgar, D. A. Mellichamp, and F. J. Doyle III, Process Dynamics and Control, 3rd ed., Hoboken, NJ: John Wiley & Sons, Inc., 2011.
Permanent Citation