The Best-Fit DDA Algorithm
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
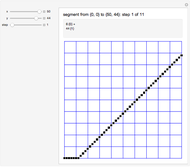
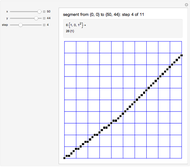
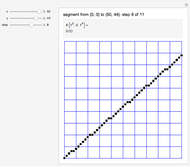
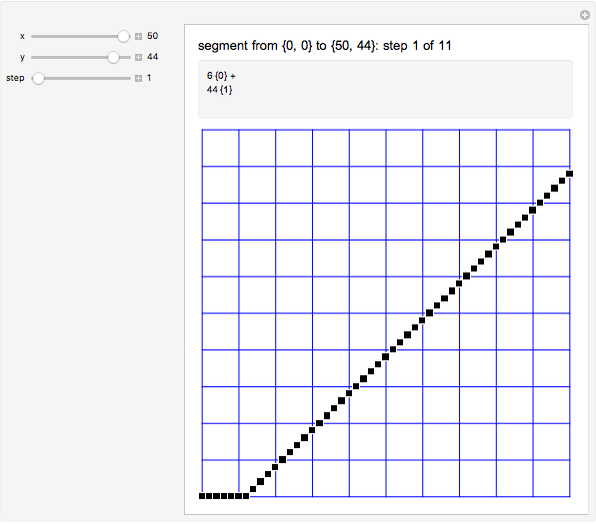
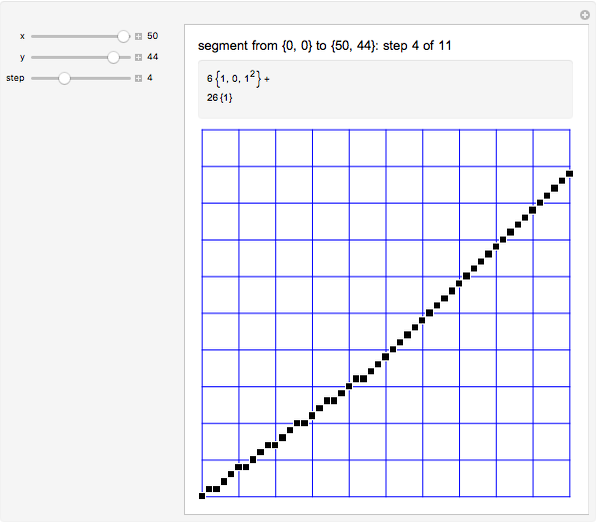
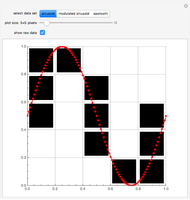
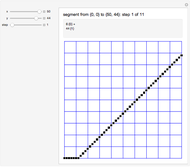
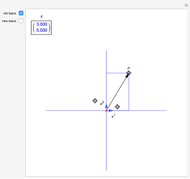
The Best-Fit DDA is an algorithm for converting a segment into a nice-looking sequence of pixels. The conversion of a segment from 
to 
with 
involves a sequence of steps. At each step the segment is approximated by the concatenation of 
copies of a path 
with 
copies of a path 
. Initially, 
, 
, 
(a single horizontal increment), and 
(a diagonal increment). Update: if 
then 
, 
, else 
, 
The algorithm terminates when 
.
Contributed by: Adriano Pascoletti (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This is a fast algorithm used in raster-scan systems. It is based on the subtractive version of Euclid's algorithm for the computation of the GCD of two positive integers 
and 
. The classical algorithm of Bresenham for drawing line segments is strictly related to the optimal placement of leap years in a cycle of 
years, and both are related to the Best-Fit DDA via Euclid's algorithm for the GCD of and and the continued fraction expansion of 
.
The Best-Fit DDA is described in Sect. 2.5 of D. Salomon, Computer Graphics and Geometric Modeling, New York: Springer-Verlag, 1999.
The Best-Fit DDA is due to C. M. A. Castle and M. L. V. Pitteway, "An Application of Euclid's Algorithm to Drawing Straight Lines," in Fundamental Algorithms for Computer Graphics, (R. A. Earnshaw, ed.), New York: Springer-Verlag, 1985 pp. 135-139.
The striking connections among Bresenham's algorithm, leap years, and Euclid's algorithm are discussed in M. A. Harris and E. M. Reingold, "Line Drawing, Leap Years, and Euclid," ACM Computing Surveys, 36(1), 2004 pp. 68–80.
Permanent Citation
Fortune's Algorithm for Voronoi Diagrams
Erik Mahieu
Bézier Curve by de Casteljau's Algorithm
Bruce Atwood
Drawing a Line on a Digital Display
Stephen Wolfram and Yu-Sung Chang
Number-Theoretic Construction of Digital Circles
Aniket Jha (BTech Student IIT KGP), Partha Bhowmick (IIT KGP), and B. B. Bhattacharya (ISI Kolkata)
Rasterization of a Data Plot
Paul van der Schaaf
Polyhedra, Spheres, and Cylinders
Russell Towle
Dim City
David Corona Balcázar
Spanning Tree of Points on Sphere
Michael Schreiber
Rotational Symmetries of Platonic Solids
George Beck
Combining Two 3D Rotations
George Beck and Jeff Bryant
-
Stacks of Reflecting Plates
Adriano Pascoletti -
The Best-Fit DDA Algorithm
Adriano Pascoletti -
Elliptic Cylindrical Coordinates
Adriano Pascoletti -
The Aging Spring
Adriano Pascoletti -
Parabolic Cylindrical Coordinates
Adriano Pascoletti -
Change of Basis in 2D
Adriano Pascoletti -
Van der Pol Oscillator
Adriano Pascoletti