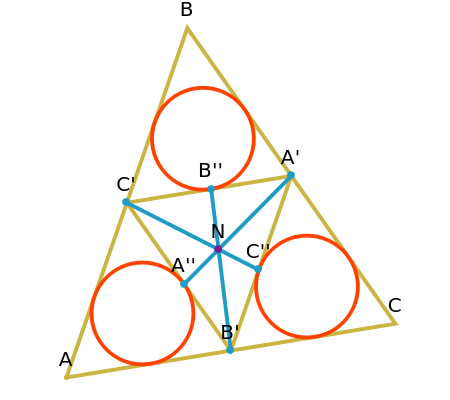Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Medial Triangle and Concurrency at the Nagel Point

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

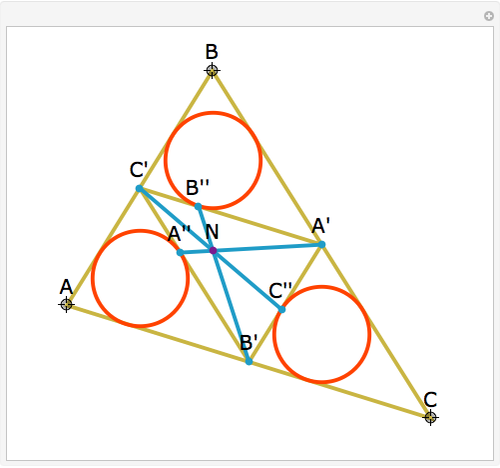
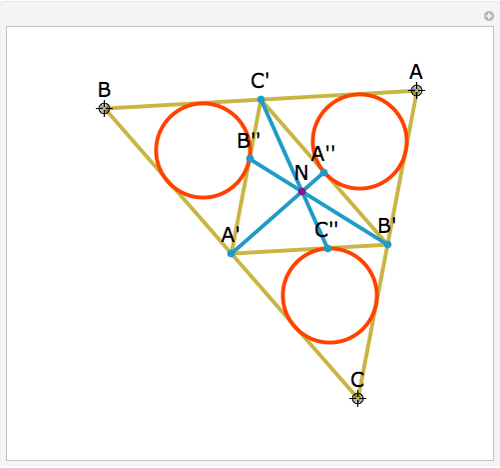
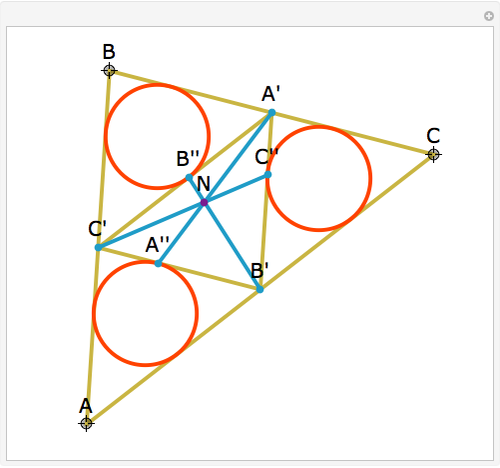
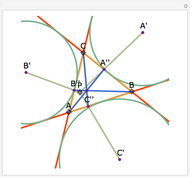
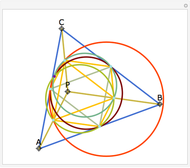
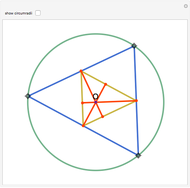
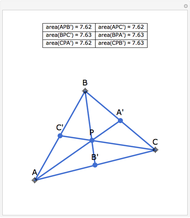
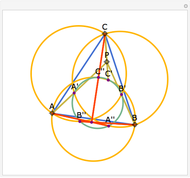
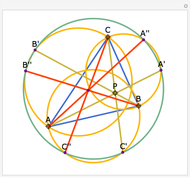
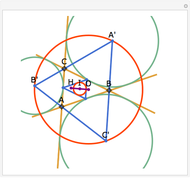
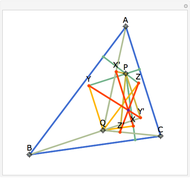
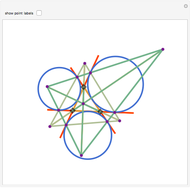
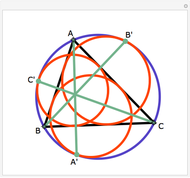
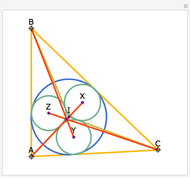
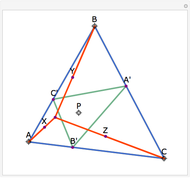
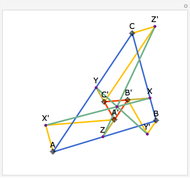
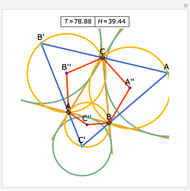
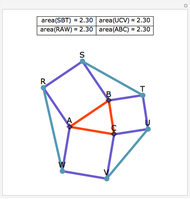
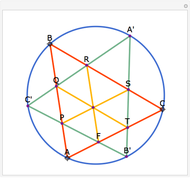
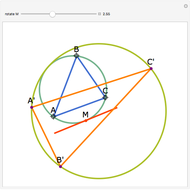
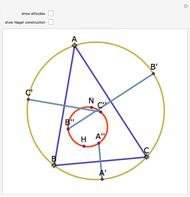
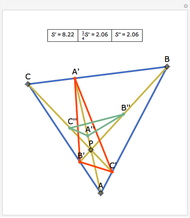
Let ABC be a triangle and A', B', and C' be the midpoints of the sides opposite A, B, and C. Let A", B", and C" be the points of tangency of the incircles of AB'C' with B'C', BA'C' with A'C', and CA'B' with A'B'. Then A'A", B'B", and C'C" are concurrent and meet at the Nagel point.

Contributed by: Jay Warendorff (March 2011)
After work by: Alexander Bogomolny
Open content licensed under CC BY-NC-SA

Snapshots

Details

The lines connecting the vertices of a triangle with the corresponding points of tangency of the three excircles are concurrent at a point called the Nagel point.

A. Bogomolny, "Nagel Point of the Medial Triangle," Interactive Mathematics Miscellany and Puzzles.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send