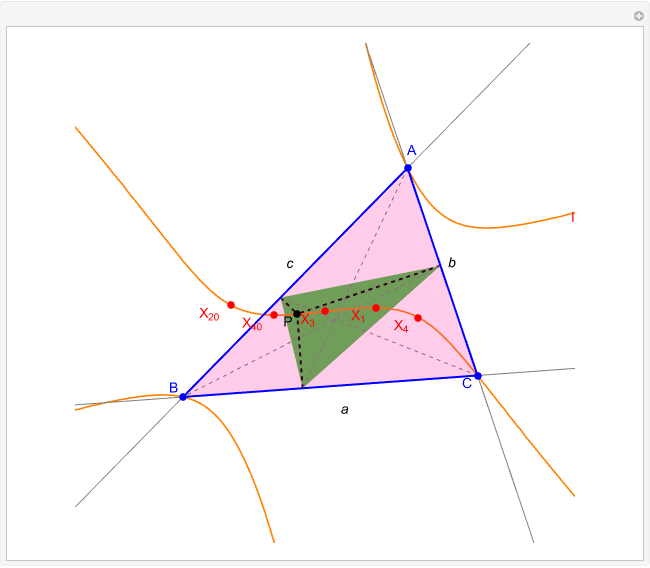
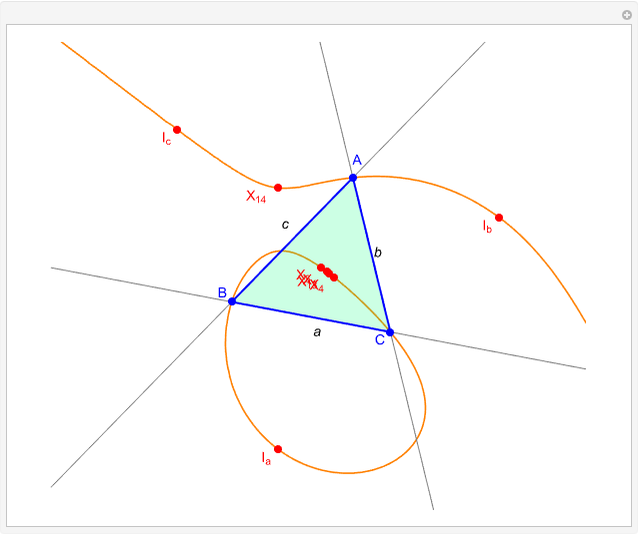
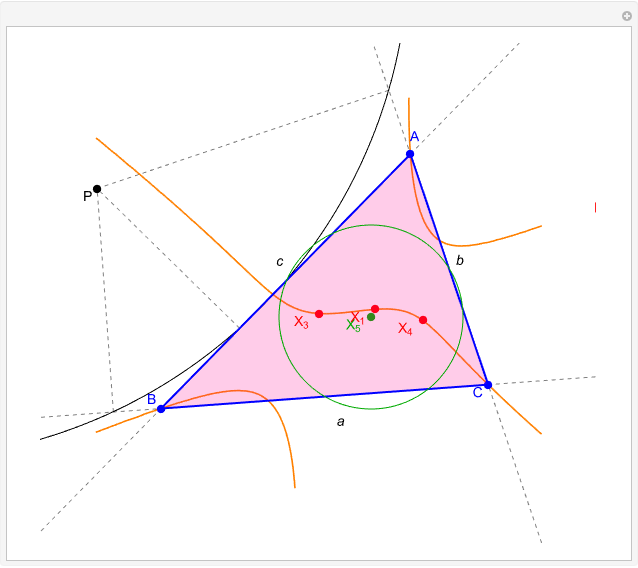
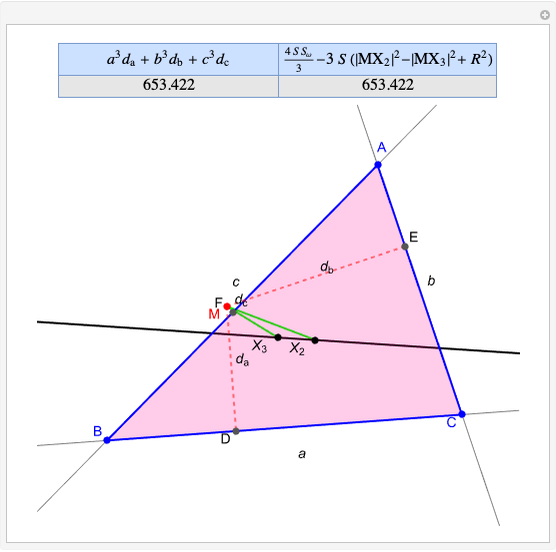
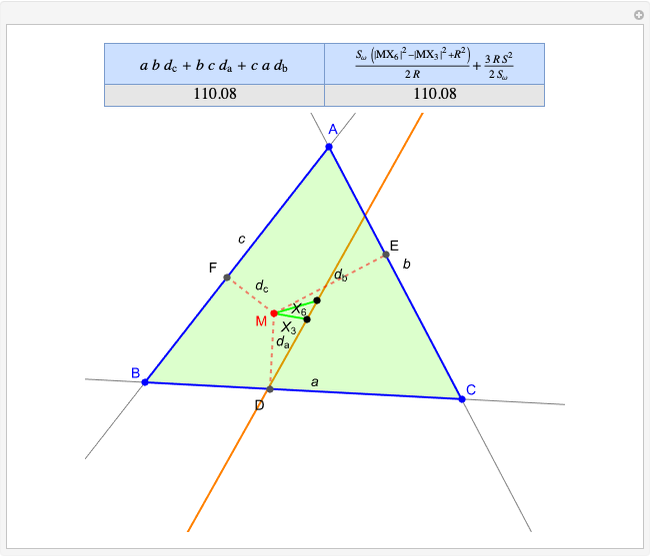
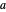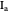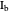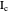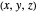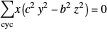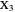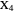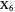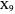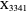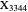Thomson Cubic

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
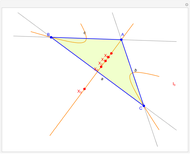
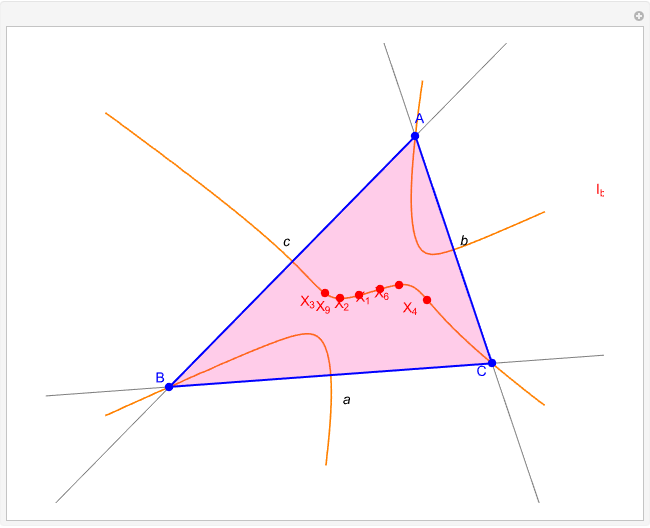
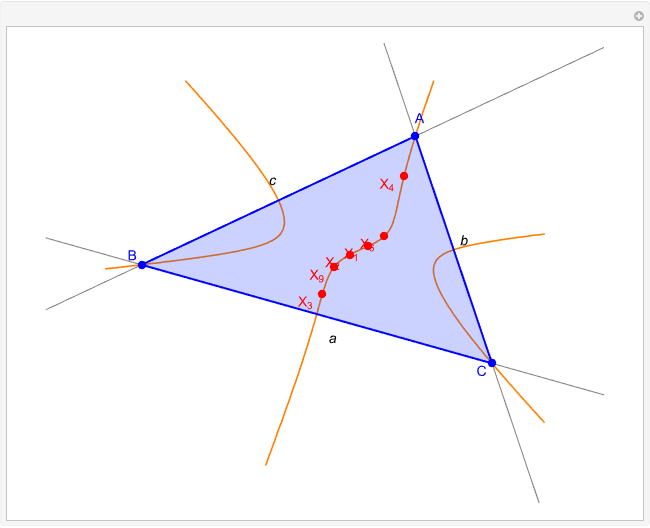
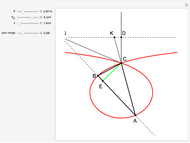
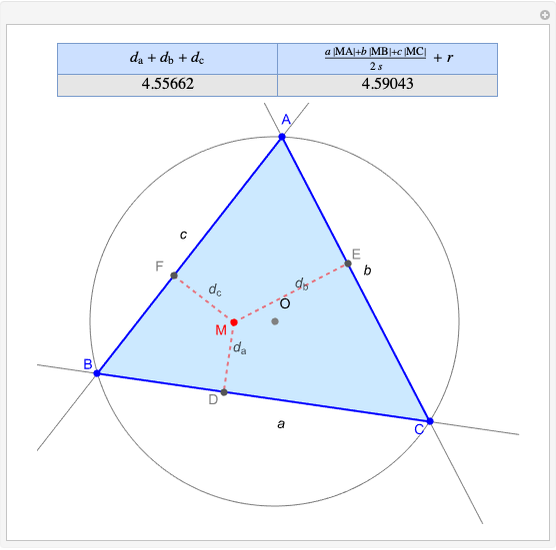
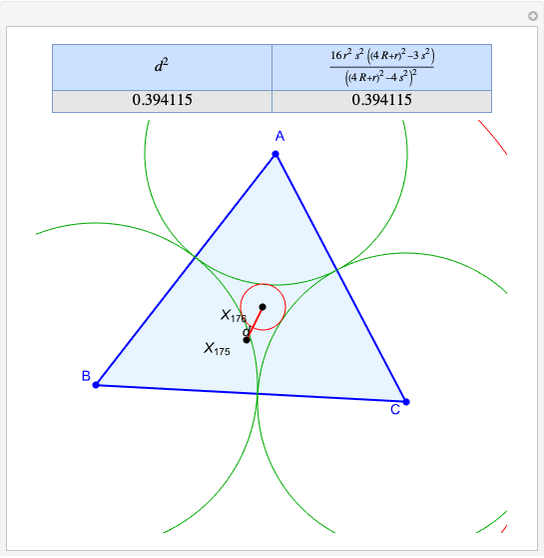
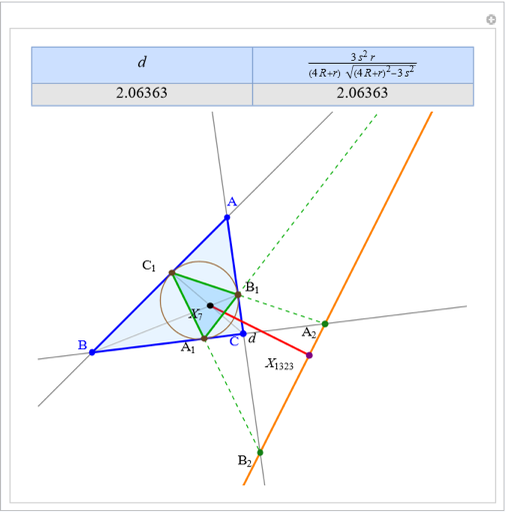
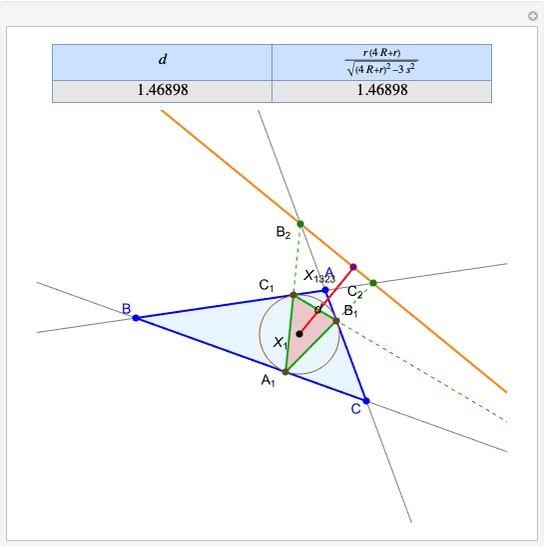
A circumconic is a conic section through the vertices of a triangle [1].
[more]
Contributed by: Minh Trinh Xuan (August 2022)
Open content licensed under CC BY-NC-SA
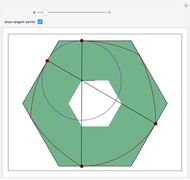
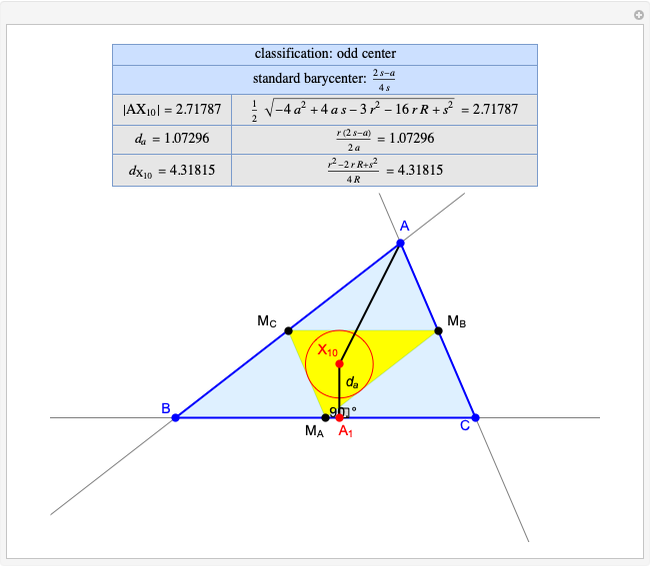
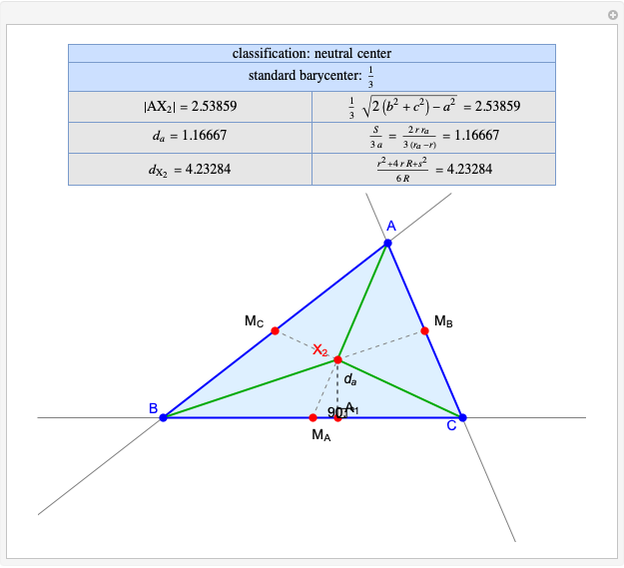
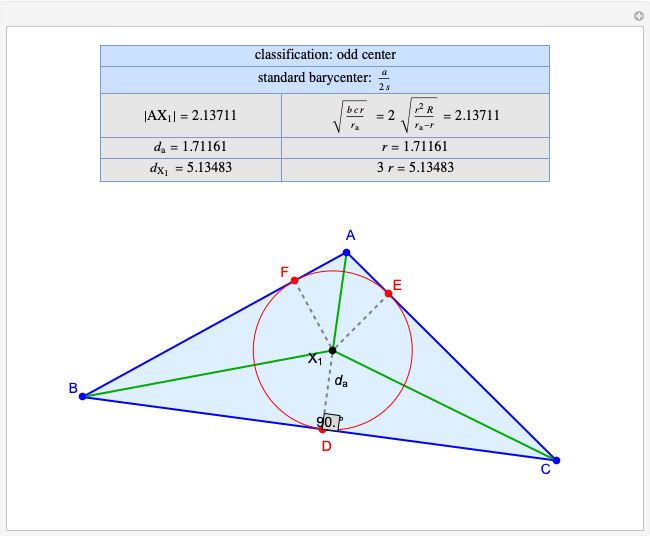
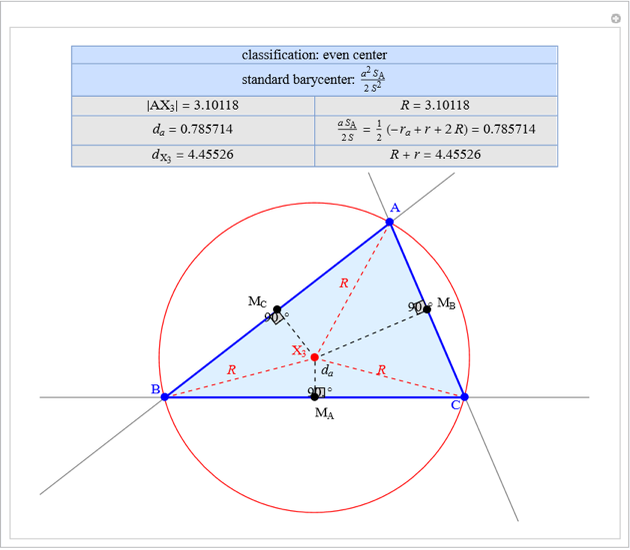
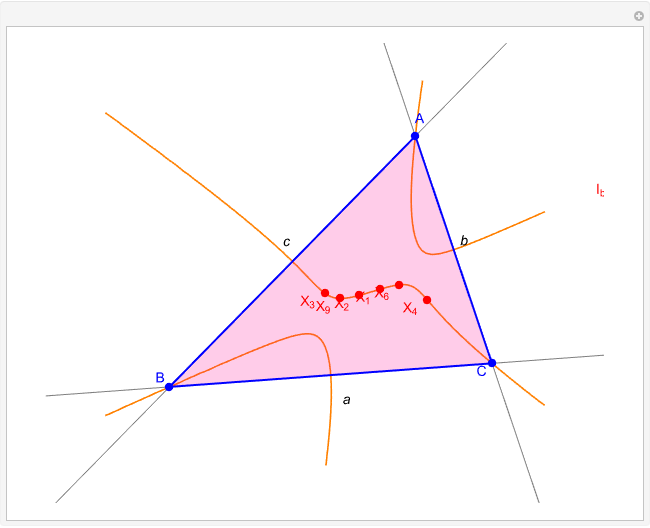
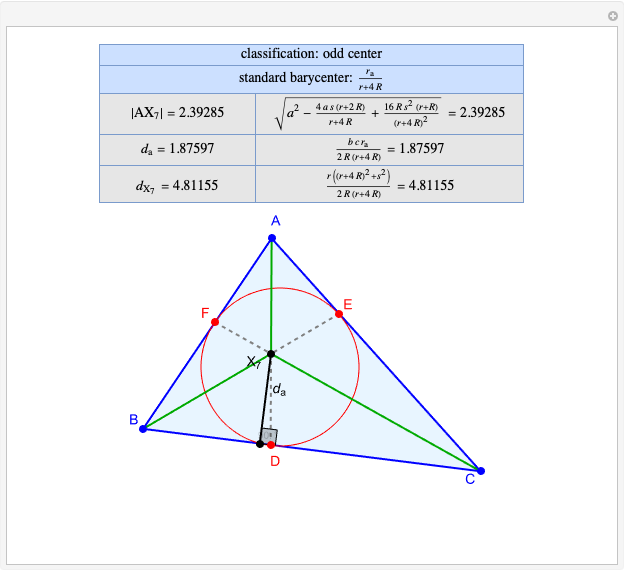
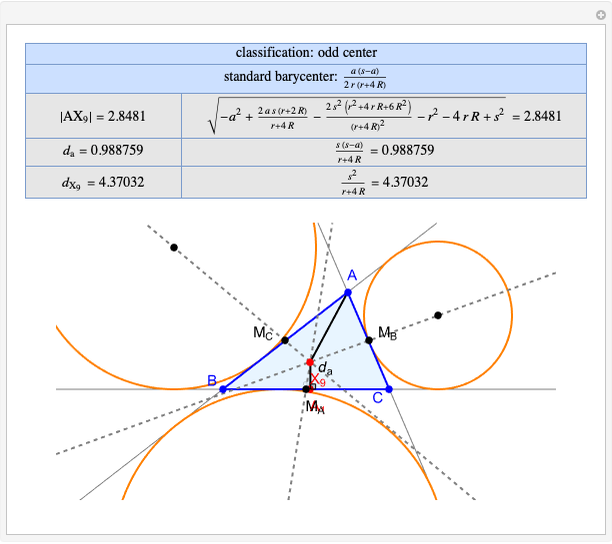
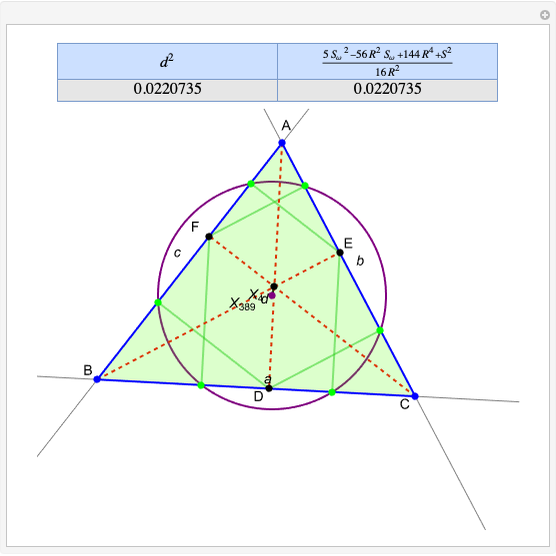
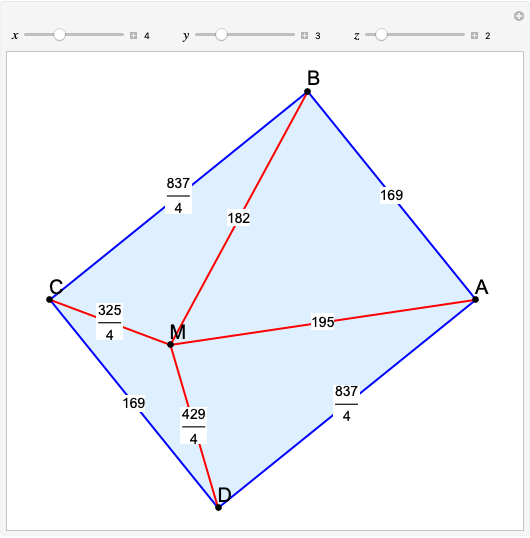
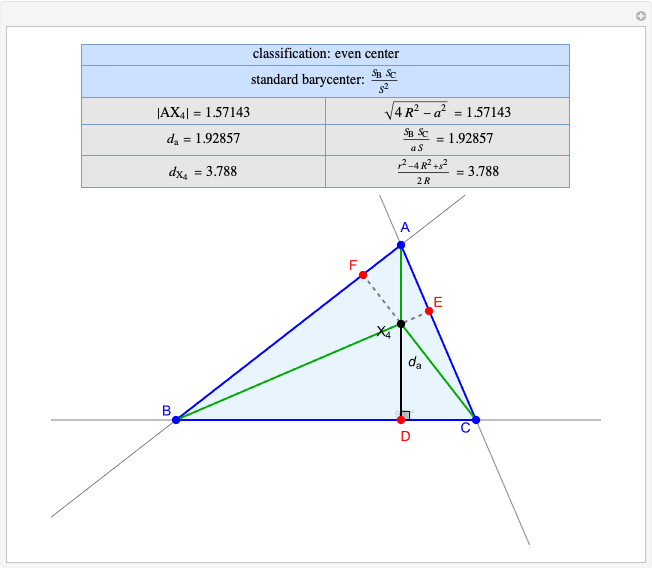
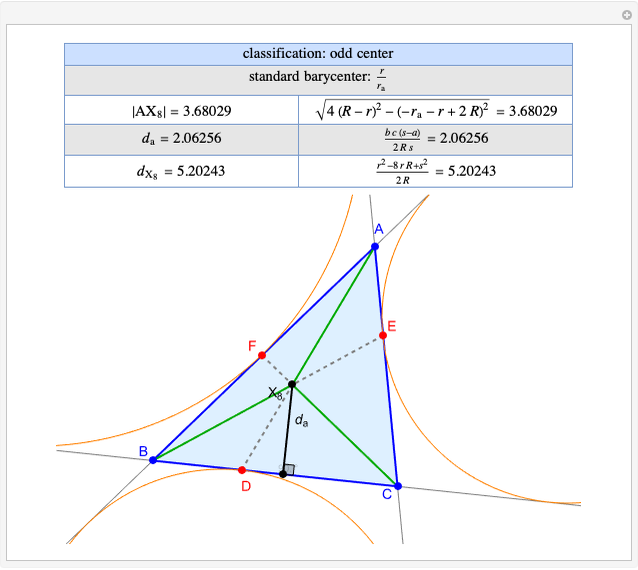
Snapshots
Details
References
[1] C. Kimberling, "Triangle Centers and Central Triangles." Congressus Numerantium, 129, 1–295, 1998.
[2] B. Gilbert. "Thomson Cubic = pK(X6,X2)." (Jul 20, 2022) bernard-gibert.pagesperso-orange.fr/Exemples/k002.html.
[3] Encyclopedia of Triangle Centers (ETC). https://faculty.evansville.edu/ck6/encyclopedia/etc.html.
[4] B. Gilbert. "Catalogue of Triangle Cubics." (Aug. 3, 2022) https://bernard-gibert.pagesperso-orange.fr/ctc.html.
Permanent Citation