Topological Phases with Quantum Walks

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
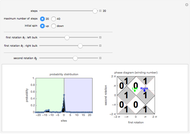
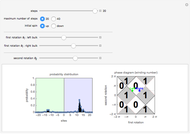
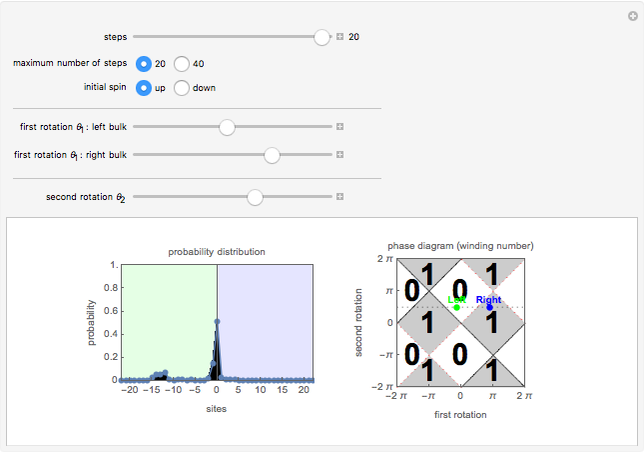
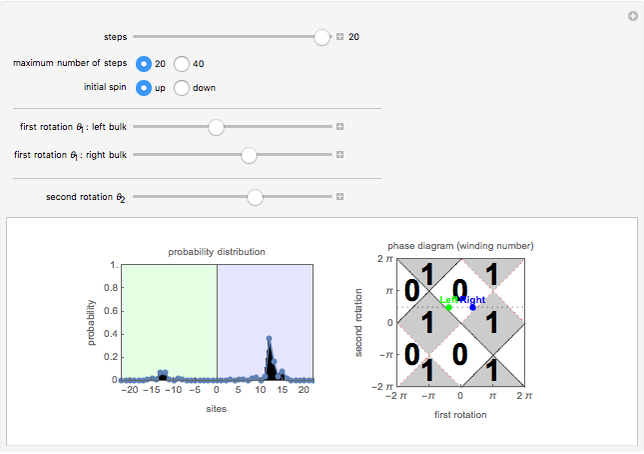
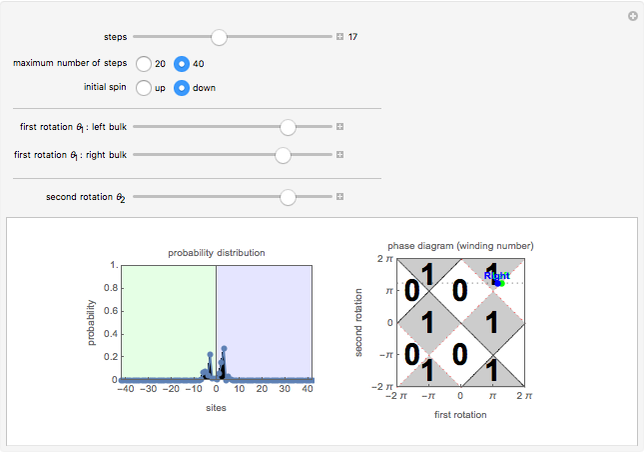
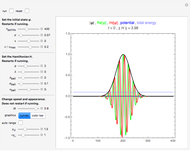
This Demonstration simulates a quantum dynamical protocol for a single spin-1/2 particle in a one-dimensional lattice, called a (split-step) discrete-time quantum walk. The dynamics generated through the quantum walk realize intriguing dynamical phases called topological phases. These phases are characterized by an integer (winding number), which can be controlled by changing the parameters of the protocols corresponding to the first and second rotation angles, 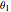 and
and  (see Details for the description of the protocol). The topological phase diagram of the quantum walk is drawn on the right.
(see Details for the description of the protocol). The topological phase diagram of the quantum walk is drawn on the right.
Contributed by: Takuya Kitagawa (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Quantum walks have attracted interest in quantum information theory as a promising toolbox for building quantum algorithms. Alternatively, seen as a quantum dynamical protocol, quantum walks also provide a versatile platform for studying exotic phases called topological phases. Topological phases are new phases of matter, and the first example of materials with this property was only found in the 1980s. Recent study of topological phases suggests that because of their unique properties, they are promising candidates for future quantum technologies such as quantum computers. Intriguingly, quantum walks give one of the simplest examples of dynamics that displays topological behavior. This Demonstration lets you explore the topological structure of (split-step) quantum walks.
The quantum walk we study in this Demonstration follows a quantum dynamical protocol defined for a single spin-1/2 particle in a one-dimensional lattice. The particle is initially placed at the origin with either spin up or spin down. Then we allow the particle to evolve by applying "one-step" operations repeatedly, and observing, for example, the resulting probability distributions. "One step" of a split-step quantum walk consists of four coherent operations:
1. Rotation of spin around the 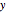 axis by angle
axis by angle 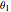 ;
;
2. Translation of spin UP to the RIGHT by one lattice site;
3. Rotation of spin around the 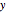 axis by angle
axis by angle  ; and
; and
4. Translation of spin DOWN to the LEFT by one lattice site.
When the second rotation  is set to 0, this split-step quantum walk reduces to a conventional, discrete-time quantum walk. The split-step quantum walks described above realize topological phases, and their phases are determined by the values of the first and second rotation angles,
is set to 0, this split-step quantum walk reduces to a conventional, discrete-time quantum walk. The split-step quantum walks described above realize topological phases, and their phases are determined by the values of the first and second rotation angles, 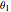 and
and  .
.
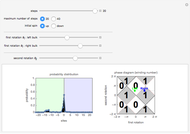
This Demonstration allows one to study the behavior of a particle under a spatially inhomogeneous quantum walk protocol. The dynamical protocol differs for the left and the right of the origin; while the second rotation is the same on the right and left regions, the first rotation angles of the left of the origin (green) and right of the origin (blue) can be chosen using the slider. Through the choices of the rotation angles, one can place the protocol of two regions in the same or different topological phases of the quantum walks. Now the Demonstration initializes the particle at the origin (boundary) with the spin either up or down, and simulates an inhomogeneous quantum walk. Interestingly, when the right and left regions correspond to quantum walk protocols with distinct topological phases, there is a finite probability that the particle remains near the origin after many steps of the quantum walk(see Snapshot 1). This bound state at the phase boundary is a manifestation of nontrivial topology of the quantum walk. For a further explanation of the physics, refer to [1].
Snapshot 1: When the left and right regions belong to different topological phases characterized by different integers, there is a topologically protected bound state at the phase boundary. Such a bound state can be detected, for example, by implementing the quantum walk with the initial particle located at the boundary. Even after many steps of the quantum walk, there remains a finite probability of finding the particle near the boundary, indicating the existence of a bound state.
Snapshot 2: When the left and right regions belong to the same topological phase, there is no bound state so that the particles rapidly fly away from the boundary.
References
[1] T. Kitagawa, M. S. Rudner, E. Berg, and E. Demler, "Exploring Topological Phases with Quantum Walks," Physical Review A 82,(3) 2010. doi: 10.1101/PhysRevA.82.033429.
[2] J. Kempe, "Quantum Random Walks: An Introductory Overview," Contemporary Physics, 44(4), July 2003, pp. 307–327.
Permanent Citation