Worm Algorithm for J-Current Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
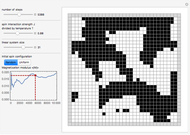
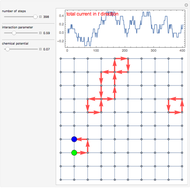
The worm algorithm is demonstrated in the case of a J-current model, a classical statistical model of currents on a lattice obeying a law of conservation. The worm algorithm is provably useful in systems whose configuration space consists of closed loops. The J-current model was originally introduced to study phase transitions in bosonic systems and is used in an extensive range of physical systems. This Demonstration can be used as an aid in understanding how the mechanisms of Monte Carlo simulation, the Metropolis algorithm, and the worm algorithm work together.
Contributed by: Darya Aleinikava (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The J-current model is a classical statistical model of conserved currents on a lattice. It was first suggested to study quantum-phase transitions in bosonic systems by mapping corresponding problems in  dimensions to the classical problem in
dimensions to the classical problem in 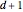 dimensions. The recently developed worm algorithm (WA) proved to be a superb tool in calculations for systems with a configuration space of closed loops, since it eliminated a critical slowdown of Monte Carlo convergence around critical points [1].
dimensions. The recently developed worm algorithm (WA) proved to be a superb tool in calculations for systems with a configuration space of closed loops, since it eliminated a critical slowdown of Monte Carlo convergence around critical points [1].
The main idea in WA is to introduce the configuration space of closed paths to collect statistics of the model. The efficiency of sampling is increased tremendously for such classical statistical models as the 2D and 3D Ising models, 2D and 3D XY models, and the Gaussian model.
This Demonstration provides a step-by-step worm algorithm implementation for a classical J-current model with a Hamiltonian of the form
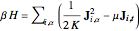 ,
,
where 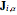 stands for a current of site
stands for a current of site 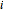 in the direction
in the direction  (either
(either  or
or  ),
), 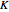 is an interaction parameter, and
is an interaction parameter, and  is a chemical potential. The variables
is a chemical potential. The variables  and
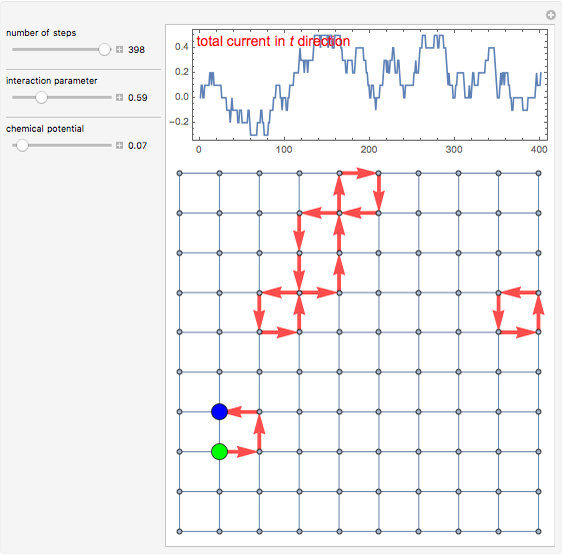
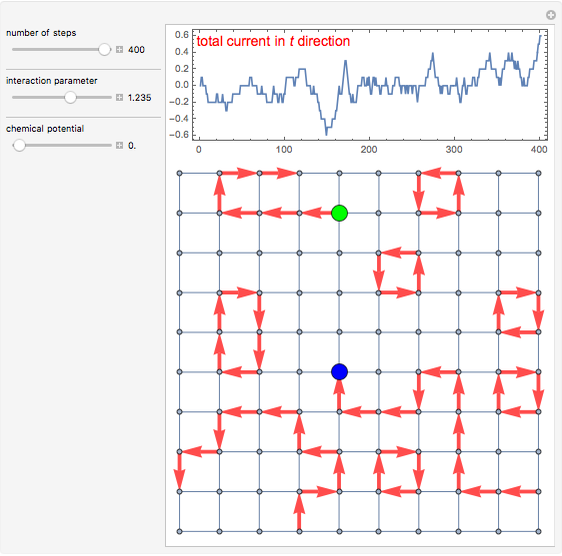
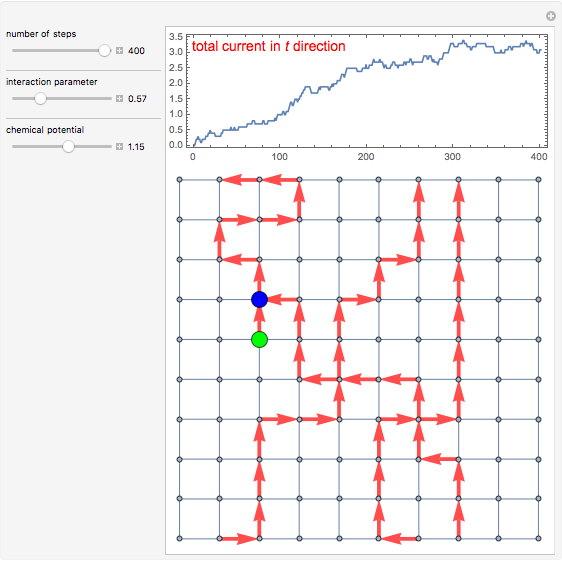
and  are the horizontal and vertical directions, respectively. We consider a 10×10 lattice, subject to periodic boundary conditions.
are the horizontal and vertical directions, respectively. We consider a 10×10 lattice, subject to periodic boundary conditions.
1. The usual scheme of the algorithm consists of choosing the initial current configuration and then performing a cycle of the usual Metropolis updates. In this Demonstration the initial configuration is  on all bonds.
on all bonds.
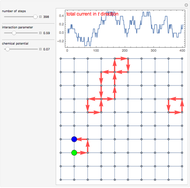
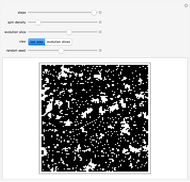
2. Closed current loops are created by starting a "worm" in the system, usually one at a time. A worm consists of a path of currents, which "wanders" around the lattice during the updates. Initially you need to choose where to place your very first worm, and once you do that you position its "head" and "tail" there (zero size worm).
3. Next you "grow" the worm head by suggesting a site around it and deciding if it should go there or not (using the Metropolis algorithm). The worm is "willing" to grow by shifting the worm head to the suggesting site thus creating a current on a bond. Such an update is called a "shift" and is one of two possible updates during WA. The described shift "draws" a new current on a bond. As you perform many of these updates and create multiple currents on bonds, it becomes possible that the worm head will try to move toward a current that already exists thus "erasing" it.
4. After wandering for a while around the lattice, the head will meet the tail and you get a closed path of currents. Such a configuration is physical and you collect the statistics for the partition function and observables at this point (however the correlator is collected at each step [1, 2]).
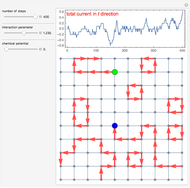
5. Once your worm is closed you can perform a second type of update called a "move": you can randomly choose another site for a worm to start and put the worm head and tail there.
6. After that, perform the procedure (steps 3–5) again.
In this Demonstration the amount of current on each bond has a maximum of 1.
Essentially WA is a draw-and-erase procedure, very similar to just drawing the loops on paper and using an eraser from time to time. It is quite efficient in sampling the system configurations and is stable enough to maintain the ergodicity of the process.
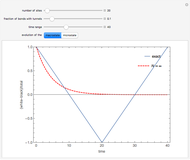
Due to periodic boundary conditions the loops can "wind" around the system, and the winding number in, for example, the  direction is defined as the total current in this direction normalized by the system's size. The winding numbers are collected only for closed-loop configurations, so they are integers and allow one to calculate, for example, the compressibility of the system.
direction is defined as the total current in this direction normalized by the system's size. The winding numbers are collected only for closed-loop configurations, so they are integers and allow one to calculate, for example, the compressibility of the system.
The lattice graph displays the bond current configuration for each step of WA and plots the graph of average current in the  direction. Such a simulation is mainly of educational value, since the number of updates is rather limited (400) and there is no chance to collect real statistics. The plot shows how the total current in the
direction. Such a simulation is mainly of educational value, since the number of updates is rather limited (400) and there is no chance to collect real statistics. The plot shows how the total current in the  direction progresses with updates. The adjustable parameters include the interaction parameter
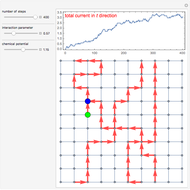
direction progresses with updates. The adjustable parameters include the interaction parameter 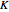 and chemical potential
and chemical potential  . You can see that for higher
. You can see that for higher 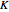 it is easier for a system to create winding loops in both directions. Chemical potential is applied in the
it is easier for a system to create winding loops in both directions. Chemical potential is applied in the  direction, so increasing
direction, so increasing  will facilitate vertical windings.
will facilitate vertical windings.
References
[1] N. Prokofev and B. Svistunov, "Worm Algorithms for Classical Statistical Models," Physical Review Letters, 87, 2001. http://link.aps.org/doi/10.1103/PhysRevLett.87.160601.
[2] "Worm Algorithm and Diagrammatic Monte Carlo." (Sep 13, 2011) http://mcwa.csi.cuny.edu/umass/index.html.
Permanent Citation