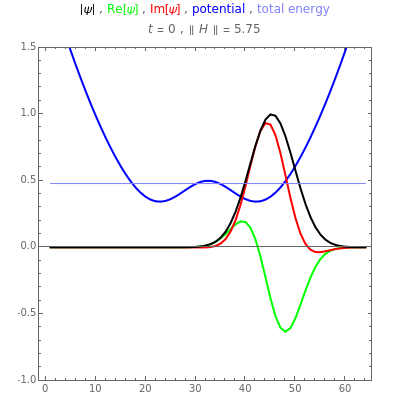
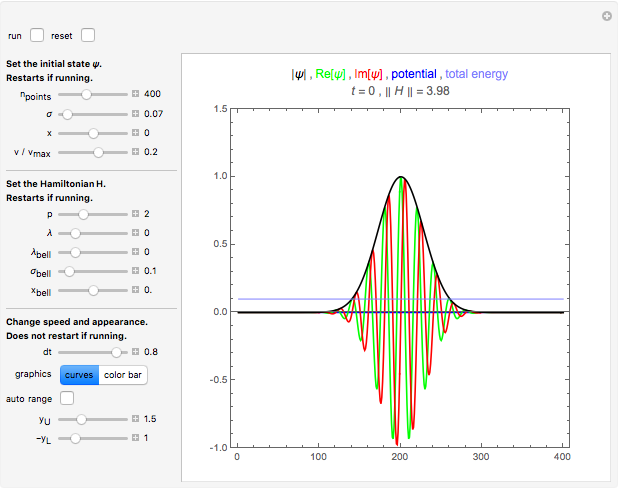
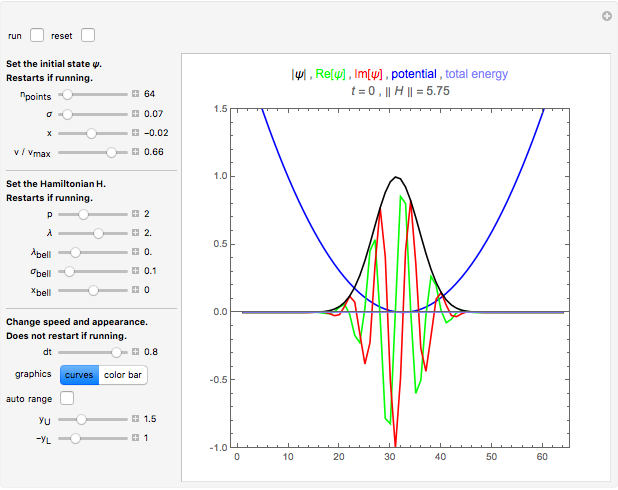
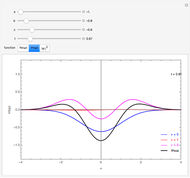
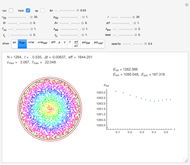
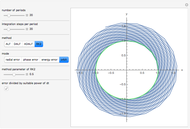
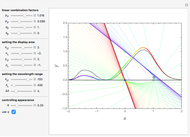
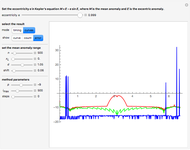
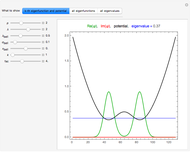
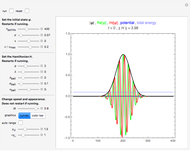
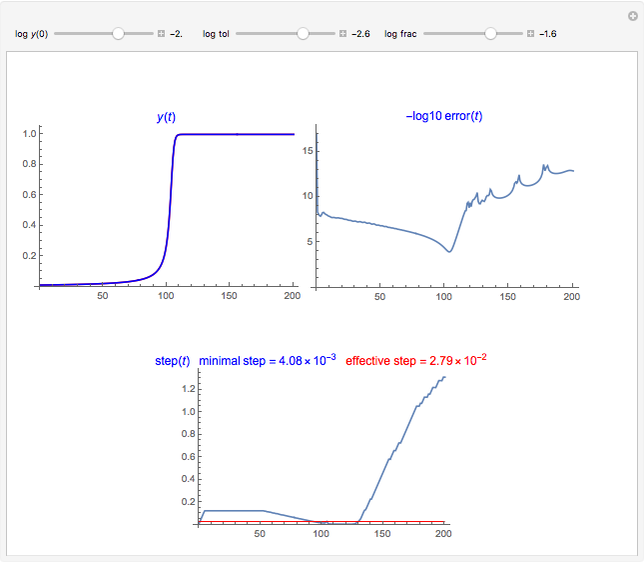
This Demonstration simulates the motion of a quantum particle in a one-dimensional periodic domain under the influence of a potential. You can set both the initial state wavefunction and the potential with sliders. Using the "dt" slider, you can change the time step even while running. Negative values of the time step let the motion go backward so that the initial state can be restored with high precision. Changing the time step is implemented such that numerical stability is guaranteed for all settings. Therefore, deviations from normalization and from energy conservation always remain small. For the graphical representation of the complex wavefunction, you can select between the real part, imaginary part, and absolute value as curves, or, alternatively, show color-coded complex numbers distributed over a stripe. The meaning of each control is described by a tooltip. The autorun feature clearly shows the available forms of the initial wavefunction and of the potential. The expectation value of the total particle energy is marked as a horizontal line in light blue. Where this line intersects the blue potential curve, there is a turning point of classical motion. Notice that the dynamics of a wavefunction in a potential is a causal dynamical system. Observing how a wavefunction reacts in the presence of potential walls and wells may give insight into the deterministic aspect of quantum mechanics. However, the "quantum measurement" problem still awaits our understanding.