Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tracer Response in a Packed Bed Reactor

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

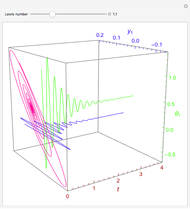
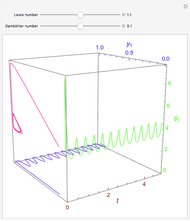
Consider an isothermal packed bed reactor (PBR) of length . Assume that a tracer pulse enters at , with . For a closed-closed vessel, the Danckwerts boundary conditions apply: and . Initially, . The turbulent flow of the fluid in the pipe is characterized by the velocity .

[more]

The tracer profile in this PBR is governed by the following partial differential equation:

, , and ,

where is a dispersion coefficient (expressed in ) that takes into account longitudinal mixing in the pipe.

Introduce the dimensionless variables and parameters: , , , , and (Péclet number).

The dimensionless governing equation becomes:

.

This Demonstration plots the tracer response curve. The experimental and theoretical [1, 2] values of the variance are reported. The two values agree closely. We also compute the skewness of the curve. This parameter is positive, indicating that the tracer distribution is skewed to the right.

[less]

Contributed by: Housam Binous, Farrukh Shehzad, Mohammad Mozahar Hossain, Abdullah A. Shaikh, and Ahmed Bellagi (January 2016)
(King Fahd University of Petroleum and Minerals, KSA; ENIM, University of Monastir, Tunisia)
Open content licensed under CC BY-NC-SA

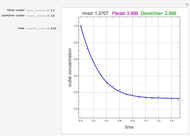
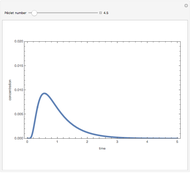
Snapshots

Details

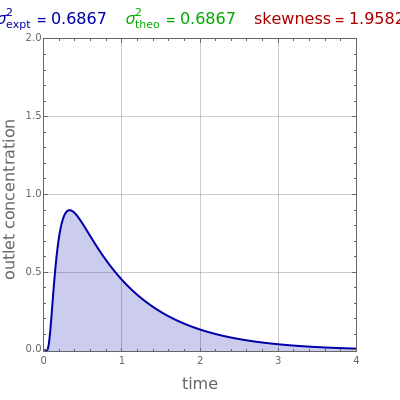
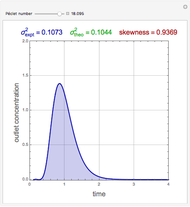
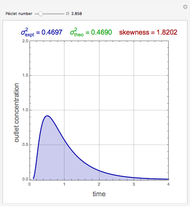
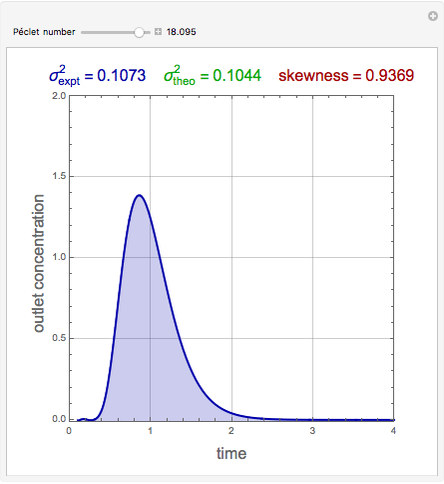
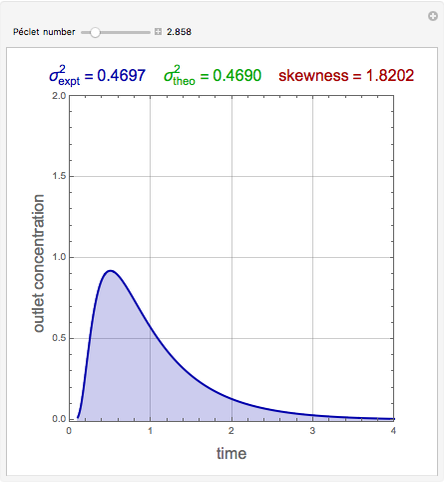
The theoretical value of the variance was first derived by van der Laan [2] in 1958:

.

References

[1] O. Levenspiel, Chemical Reaction Engineering, New York: John Wiley & Sons, 1999.

[2] E. T. van der Laan, Chemical Engineering Science, 7(3), 1958 pp. 187–191. doi:10.1016/0009-2509(58)80025-1.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send