Twisted Surfaces of Revolution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
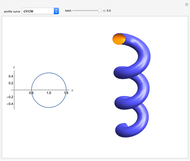
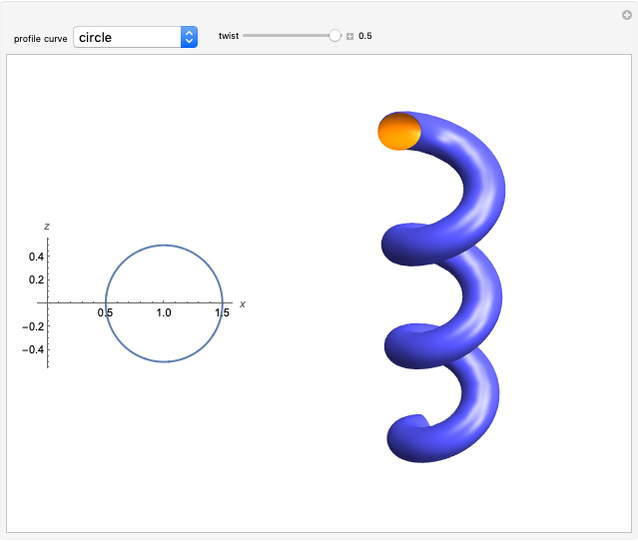
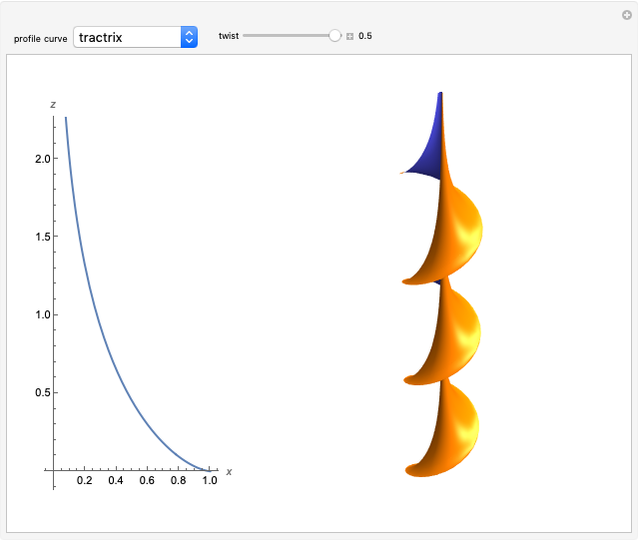
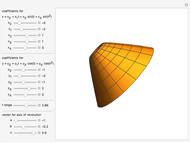
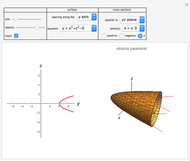
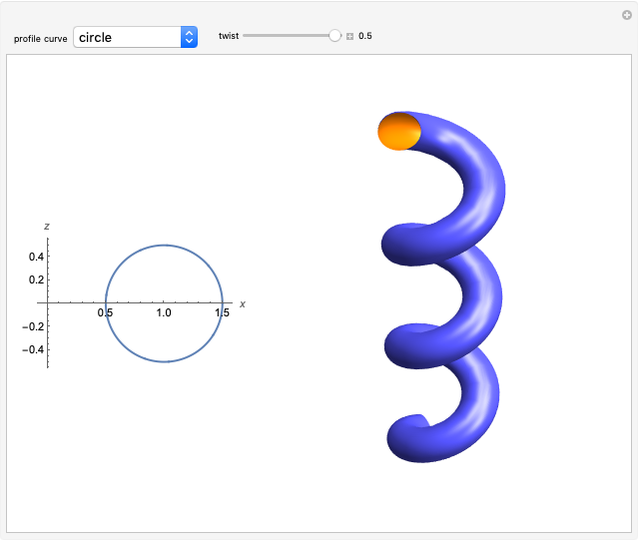
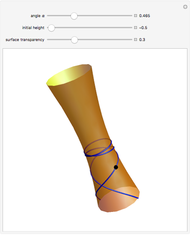
This Demonstration shows several examples of twisted surfaces of revolution (also known as generalized helicoids). The surfaces are generated by taking a profile curve in the  -
- plane, rotating it around the
plane, rotating it around the  axis and, at the same time, translating it parallel to the same axis. Thus, the profile traces a circular helix.
axis and, at the same time, translating it parallel to the same axis. Thus, the profile traces a circular helix.
Contributed by: Antonin Slavik (August 2022)
(Charles University, Prague)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Assuming that the parametrization of the profile curve is
 ,
,
the corresponding twisted surface of revolution has parametrization
 ,
,
where  is the amount of twisting (
is the amount of twisting ( yields an ordinary surface of revolution).
yields an ordinary surface of revolution).
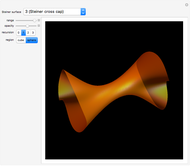
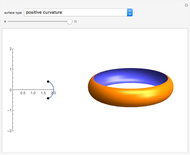
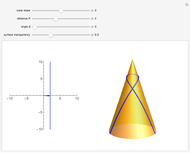
The first three of the six examples in this Demonstration are particularly noteworthy:
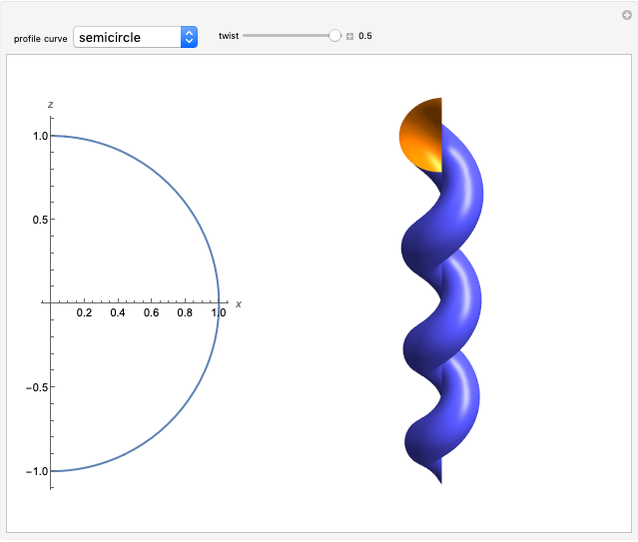
"semicircle" has its center on the  axis and gives a corkscrew surface (twisted sphere);
axis and gives a corkscrew surface (twisted sphere);
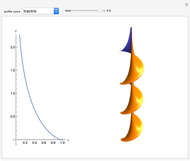
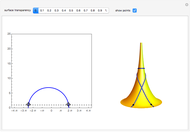
"tractrix" is a Dini's surface (twisted pseudosphere) that is a well-known example of a surface with constant negative Gaussian curvature;
"zero-curvature" is the curve with
 ,
,
 ,
,
that produces a surface with constant zero Gaussian curvature.
See, for example, [1, Chapter 15] and [2, Exercise 4.46].
References
[1] A. Gray, E. Abbena and S. Salamon, Modern Differential Geometry of Curves and Surfaces with Mathematica, 3rd ed., Boca Raton, FL: Chapman & Hall/CRC, 2006.
[2] K. Tapp, Differential Geometry of Curves and Surfaces, New York: Springer Science+Business Media, 2016.
Permanent Citation