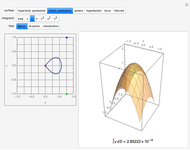
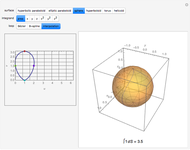
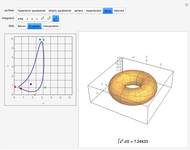
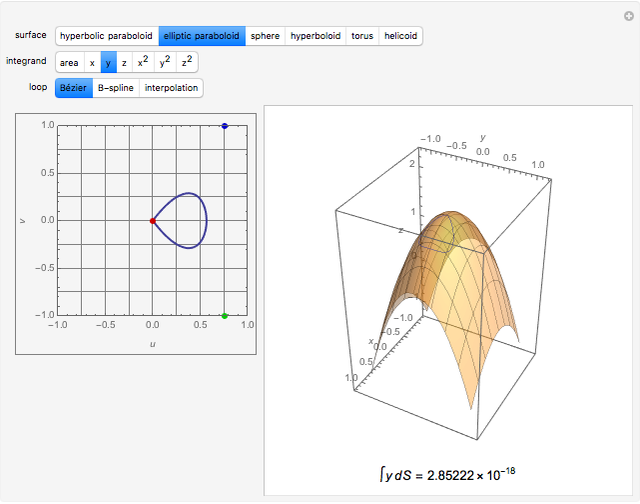
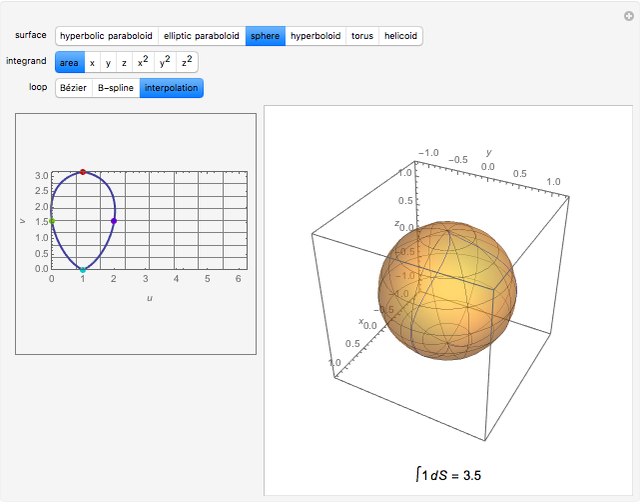
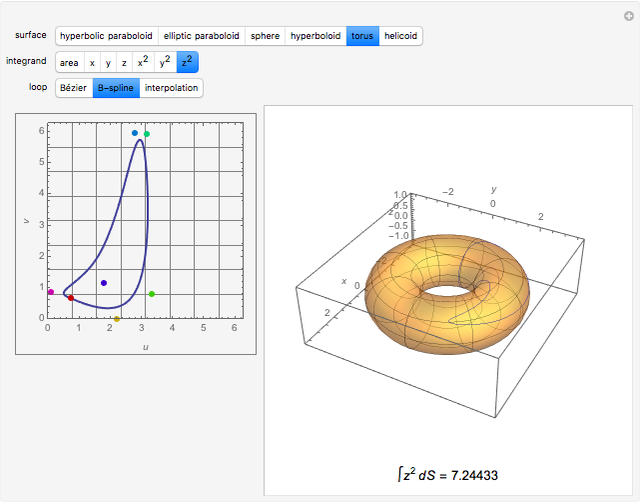
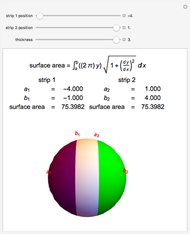
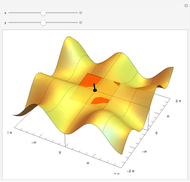
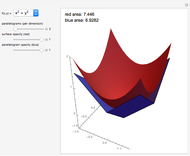
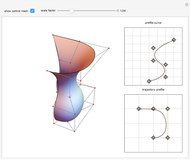
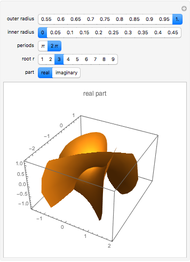
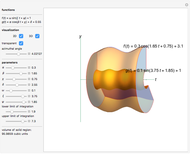
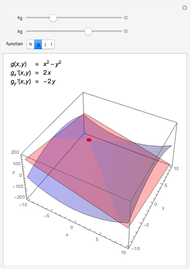
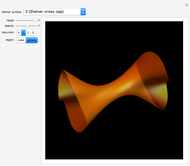
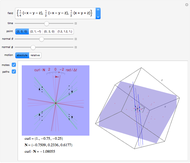
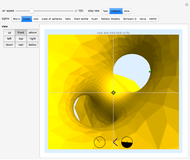
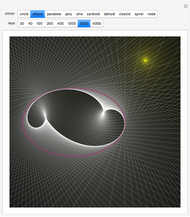
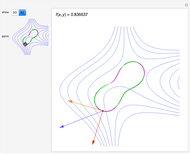
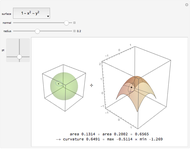
Compute the integral of the integrand over the part of the surface bounded by the loop defined by the movable locators in the domain on the left. Be aware that the orientation of the loop is significant. If a loop is not a counterclockwise, simple, closed curve, then the contribution to the integral of each segment cut off by the loop is multiplied by its winding number. (The orientation can be seen in the color of the points: red to green to blue, and back to red.) The points may determine a loop in three ways: a Bézier curve, a B-spline curve, or an interpolation through the points.