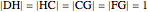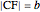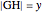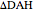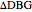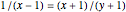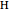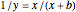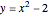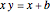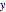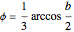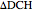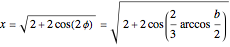Vieta's Solution of a Cubic Equation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
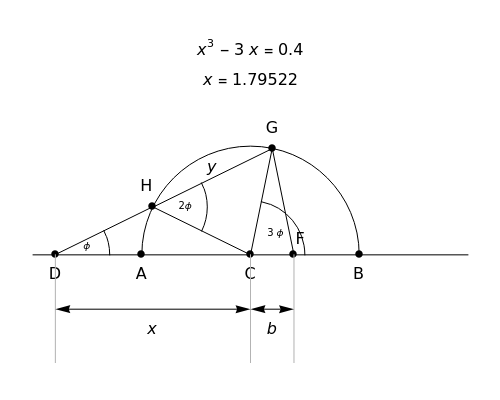
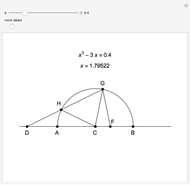
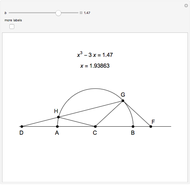
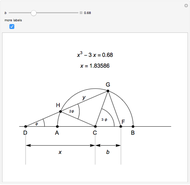
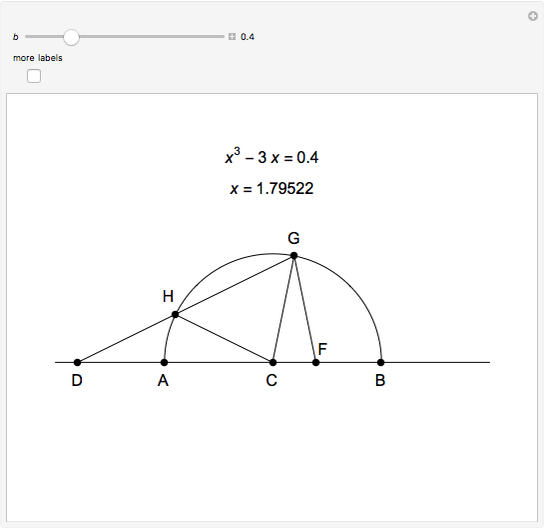
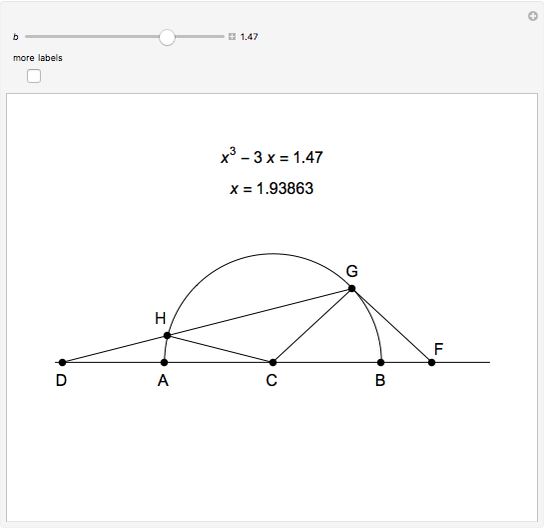
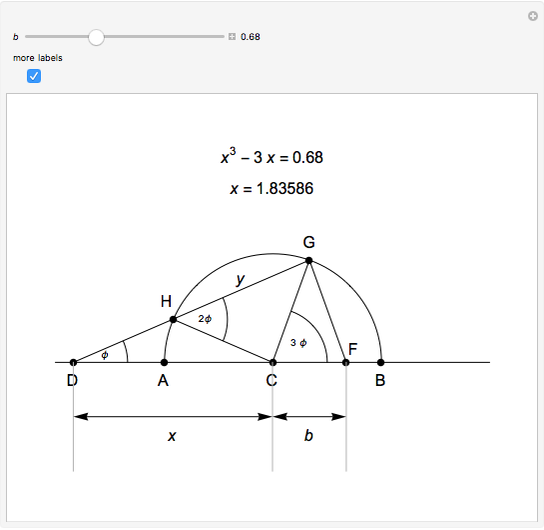
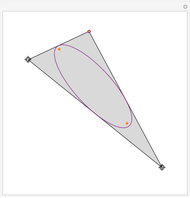
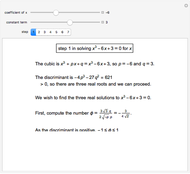
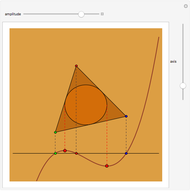
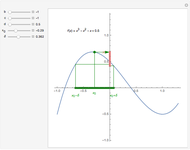
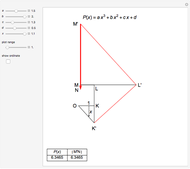
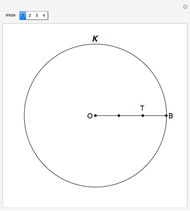
This Demonstration shows Vieta's solution of the depressed cubic equation 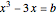 , where
, where 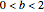 . To solve it, draw an isosceles triangle
. To solve it, draw an isosceles triangle  with base
with base  and unit legs. Let
and unit legs. Let  be the angle at the base and
be the angle at the base and 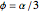 . Draw a second isosceles triangle
. Draw a second isosceles triangle 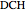 with base angle
with base angle  and unit legs. The base of the second triangle is a root of the equation.
and unit legs. The base of the second triangle is a root of the equation.
Contributed by: Izidor Hafner (October 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998 pp. 126–140.
[2] M. Hladnik, "Some Historical Constructions of the Regular Heptagon" (in Slovenian), Obzornik za matematiko in fiziko, 61(4), 2014 pp. 132–145. www.obzornik.si/61.
Permanent Citation