Vieth-Müller Circles (Visual Depth Perception 8)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
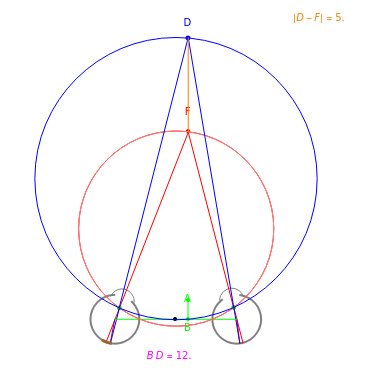
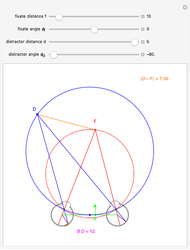
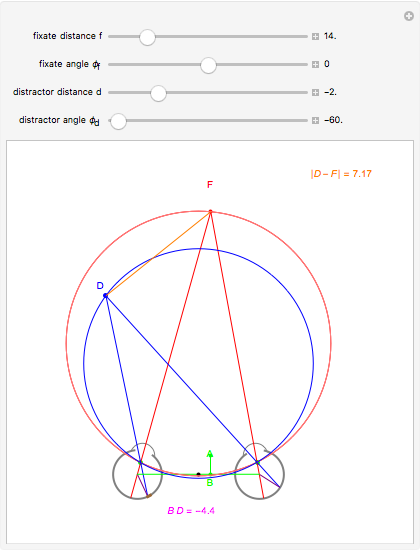
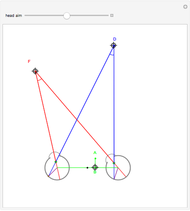
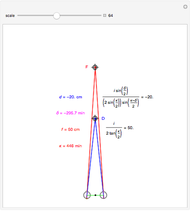
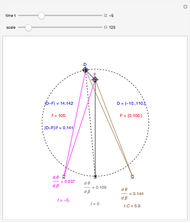
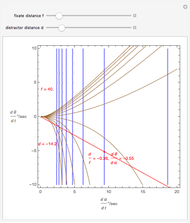
This Demonstration shows that binocular disparity is constant on the blue circles through one distractor and the eye nodes. The sliders allow you to set a distance 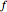 for the fixate point F away from the base point, and a distance
for the fixate point F away from the base point, and a distance  for the distractor D beyond it. The scale is very small to exaggerate the angles in order to see what they measure at normal viewing distances.
for the distractor D beyond it. The scale is very small to exaggerate the angles in order to see what they measure at normal viewing distances.
Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
One of the main goals of this set of Demonstrations, outlined in the first Demonstration, "Motion/Pursuit Law in 1D (Visual Depth Perception 1)" (see Related Links), is to show which geometric inputs to vision determine the depth of objects and especially the depth of D relative to F.
The fact that binocular disparity does not vary around the circles shown in this Demonstration implies that it is not a good measure of the distance of D beyond F unless D and F are on the 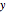 axis.
axis.
Even when D and F are on the 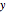 axis, binocular disparity alone does not determine depth. The Demonstration "Binocular Disparity versus Depth (Visual Depth Perception 9)" (see Related Links) allows you to vary the depth along a curve of constant binocular disparity. The Demonstration "Disparity, Convergence, and Depth (Visual Depth Perception 10)" (see Related Links) gives the depth formula.
axis, binocular disparity alone does not determine depth. The Demonstration "Binocular Disparity versus Depth (Visual Depth Perception 9)" (see Related Links) allows you to vary the depth along a curve of constant binocular disparity. The Demonstration "Disparity, Convergence, and Depth (Visual Depth Perception 10)" (see Related Links) gives the depth formula.
The remainder of this notebook proves the geometric lemma that binocular disparity is constant on circles through the eye nodes.
The Circle Lemma
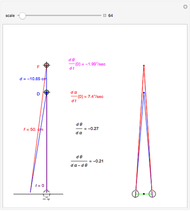
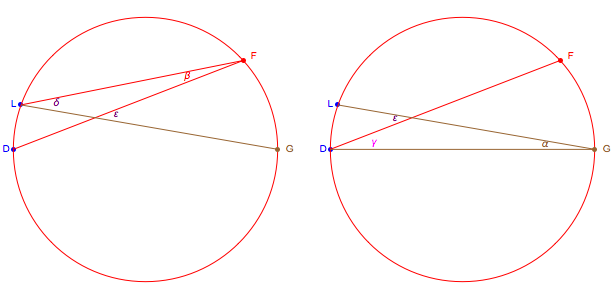
Following is a proof that convergence angles are the same for every point on a circle through both eye nodes and one point (either the fixate or the distraction). This means any distraction point on the circle through the fixate has retinal disparity zero. This is the Vieth-Müller circle, but more: any point on the circle through one distraction and both nodes has the same retinal disparity as any other distraction on this circle because they have the same convergence angle.
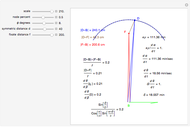
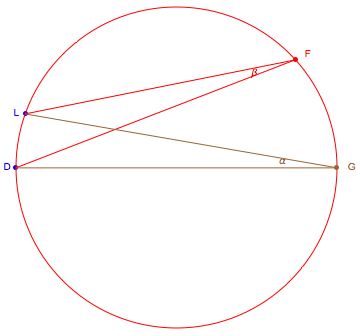
We will prove the theorem for half the convergence angle, taking a point F on the circle and the rays to one point L that corresponds to the left node and another point D on a horizontal diameter to G.
Our goal is to show the angle  at G equals the angle
at G equals the angle  at F.
at F.  is just half of the convergence angle to both nodes and the diameter helps with the proof.
is just half of the convergence angle to both nodes and the diameter helps with the proof.
We add radial segments from the center to the points as shown in green and magenta. The resulting isosceles triangles show that the angles marked  are equal and that
are equal and that  occurs on the left as shown in green near L. The angles marked
occurs on the left as shown in green near L. The angles marked  are equal because they are on opposite sides of crossing lines.
are equal because they are on opposite sides of crossing lines.
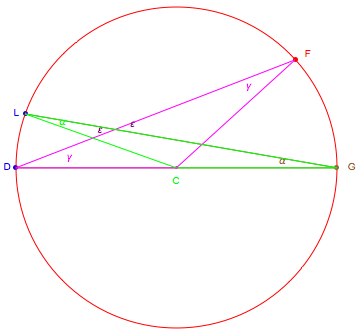
Now use the isosceles triangle LCF to see that 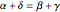 for the angle
for the angle  shown next.
shown next.

The sum of the angles of a triangle is  , so
, so 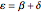 and
and  , so
, so  .
.
Combining the last two results and subtracting,
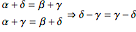 so
so 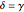 and
and  .
.
The convergence angles are always the same on circles through the two nodes and the point. Convergence angles are the same at every point of the blue circle, so the difference between convergence angles for points on the blue circle and the convergence angle of the fixate is the same: 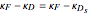 .
.

This constant disparity circle is shown interactively in the Demonstration.
NOTE: moving the fixate on the Veith–Müller circle (through the fixate) will change that circle slightly because the eye nodes move to follow the fixate.
For more information on the Vieth–Müller circle (or horopter) see the Wikipedia page.
Permanent Citation