Disparity, Convergence, and Depth (Visual Depth Perception 10)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
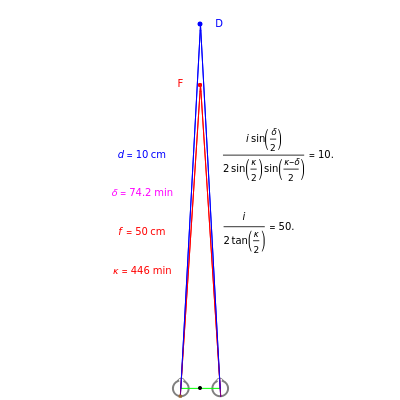
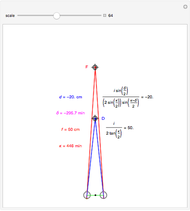
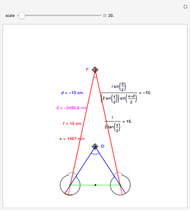
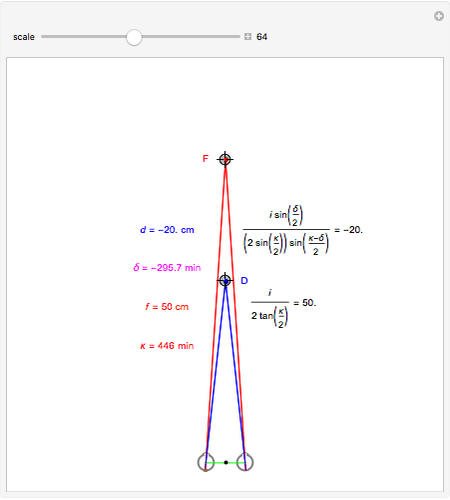
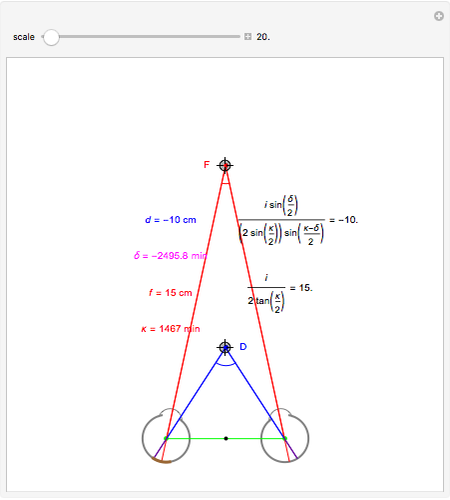
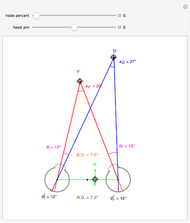
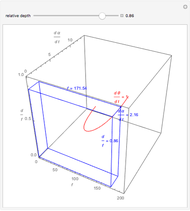
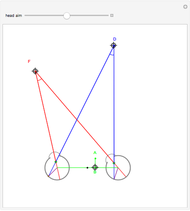
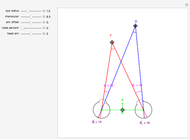
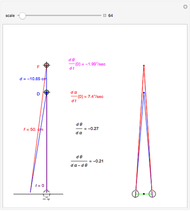
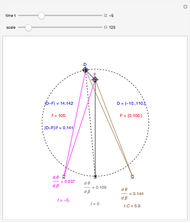
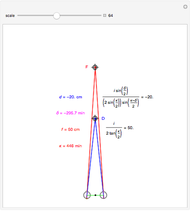
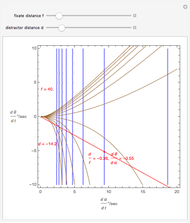
This Demonstration shows binocular disparity together with the convergence angle required for the eyes to fix on F. The angles  and
and  together determine the depth of objects on the
together determine the depth of objects on the  axis.
axis.
Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
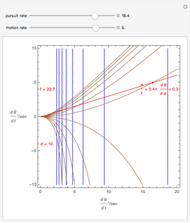
Binocular disparity has been studied since Euclid, but was popularized by Wheatstone about 150 years ago with the invention of the stereoscope. A stereoscope shows two slightly different images to the separate eyes and gives the scene the appearance of depth. However, disparity alone does not determine depth, as shown in the Demonstration "Binocular Disparity versus Depth (Visual Depth Perception 9)" (see Related Links). To simplify derivations for this Demonstration we take no aim offset and set the nodePercent equal to zero, that is, nodes are (unrealistically) at the center of the eye.
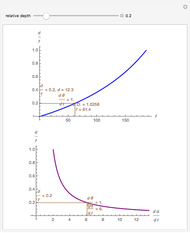
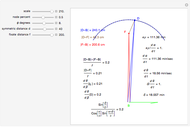
The exact formula for depth when the fixate and distraction are on the  axis (including sign) from
axis (including sign) from 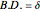 (in radians) for a given fixate distance
(in radians) for a given fixate distance  is given by the following formula with interocular distance
is given by the following formula with interocular distance  :
:
 .
.
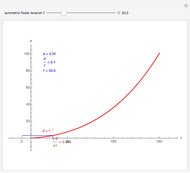
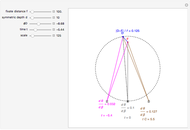
Binocular disparity does not determine depth since it requires the absolute fixate distance  . The value of
. The value of  could come from a convergence cue since the convergence angle
could come from a convergence cue since the convergence angle  of the eyes is related to fixate distance by
of the eyes is related to fixate distance by
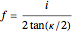 ,
,
so (after simplification) depth from static cues is
 .
.
For more information about stereoscopic vision, see the Wikipedia page.
Permanent Citation