Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Binocular Disparity (Visual Depth Perception 7)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

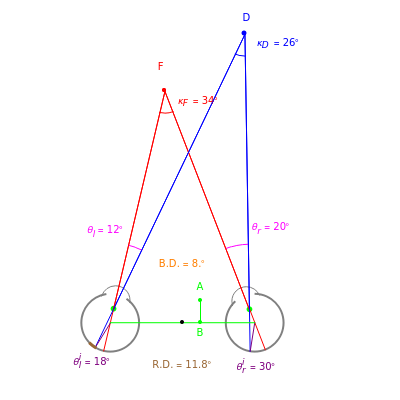
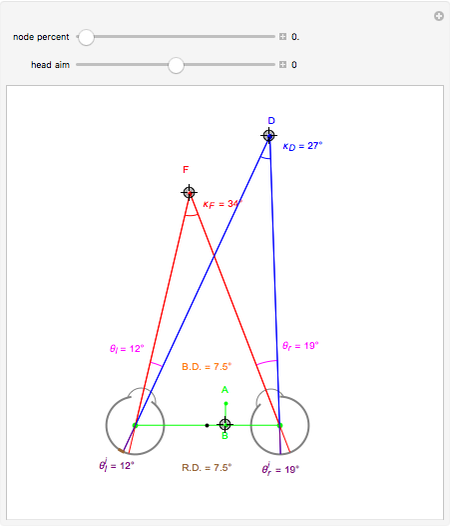
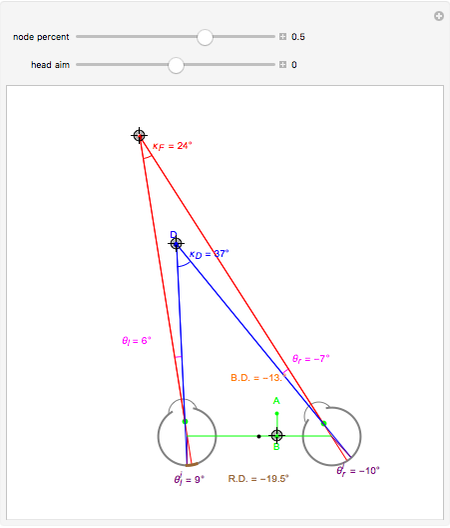
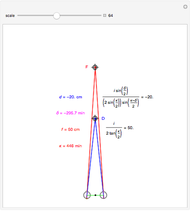
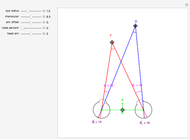
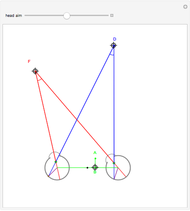
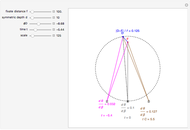
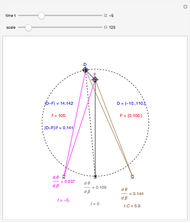
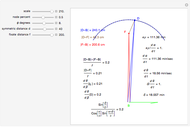
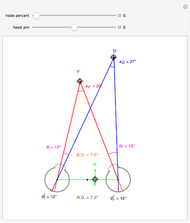
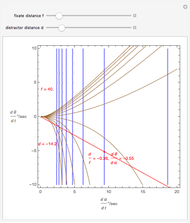
This Demonstration shows binocular and retinal disparity. Since our eyes are separated, they receive slightly different images, a "disparity". Mathematically, binocular disparity is the difference between the "convergence angles" . Binocular disparity is shown in degrees in orange. The scale is very small to exaggerate the angles in order to see what they measure at normal viewing distances.

[more]

Simple geometry shows that binocular disparity is also the signed difference of the separation angles measured counterclockwise from distraction to fixate for the two eyes, . With these sign conventions, the formula works in all cases.

The term "binocular disparity" refers to geometric measurements made external to the eye. The disparity of the images on the actual retina depends on factors internal to the eye, especially the location of the nodal points, even if the cross section of the retina is a perfect circle as in the model. The small brown segment shows the disparity between the images of the left and right eye. Notice that retinal disparity depends on the node location by sliding the "node percent" slider.

[less]

Contributed by: Keith Stroyan (March 2011)
Open content licensed under CC BY-NC-SA

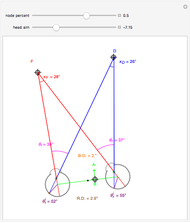
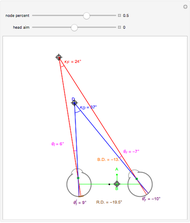
Snapshots

Details

Binocular disparity has been studied since Euclid, but was popularized by Wheatstone about 150 years ago with the invention of the "stereoscope".

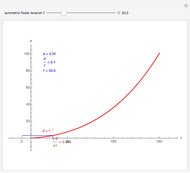
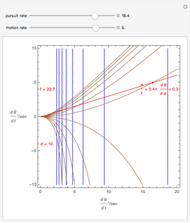
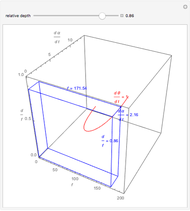
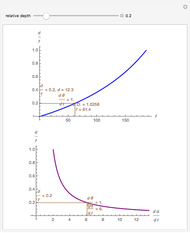
Binocular disparity is constant on circles through the node points of the eyes, as we show in the Demonstration "Vieth–Müller Circles (Visual Depth Perception 8)" (see Related Links). The connection between depth and disparity is shown in the Demonstrations "Disparity, Convergence and Depth (Visual Depth Perception 10)" and "Binocular Disparity versus Depth (Visual Depth Perception 9)" (see Related Links).

For more information on stereoscopic vision see the Wikipedia page and the introduction in the Demonstration "Motion/Pursuit Law in 1D (Visual Depth Perception 1)" (see Related Links).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send