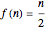Visualizing the Collatz Conjecture and Some Variants
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
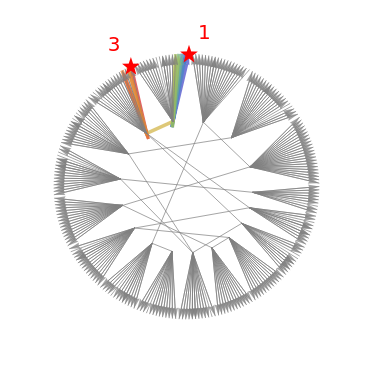
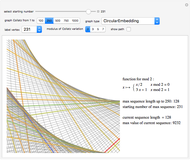
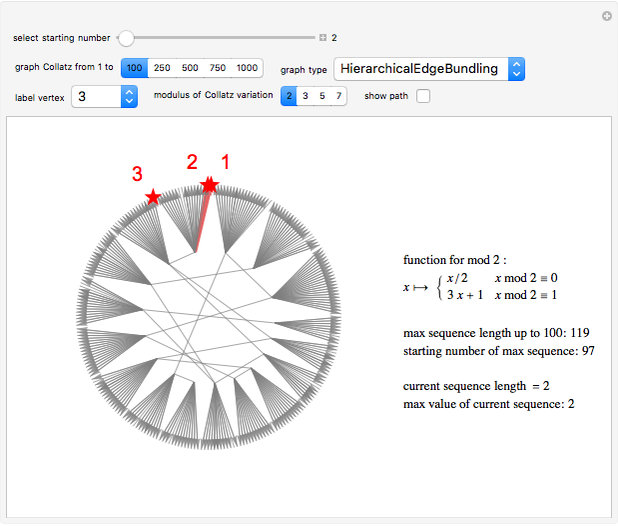
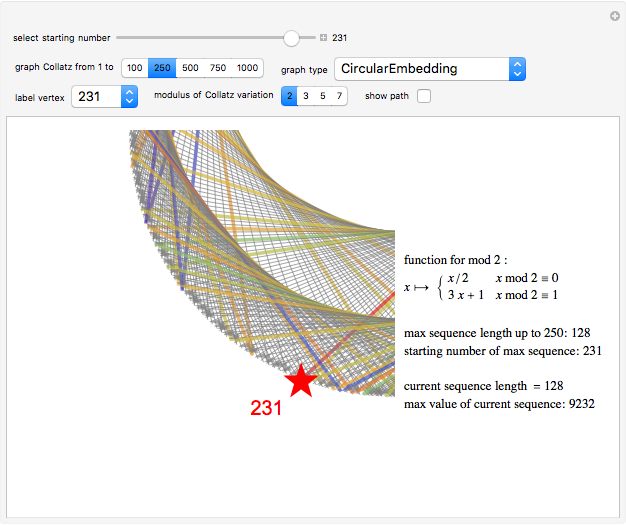
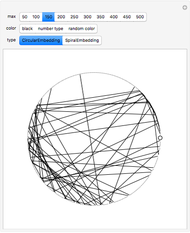
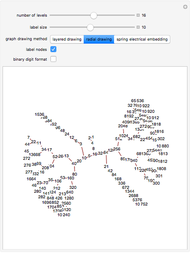
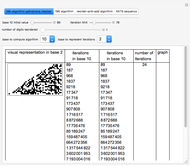
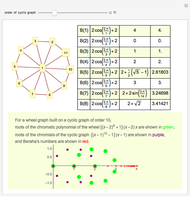
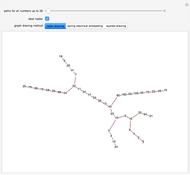
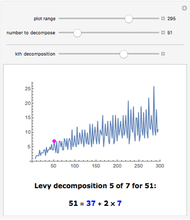
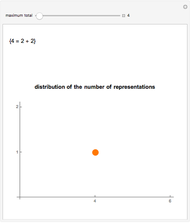
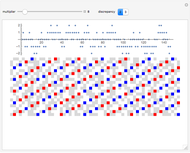
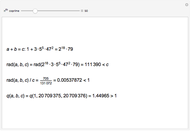
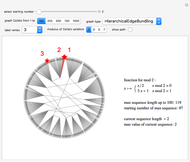
The Collatz conjecture (also known as the 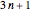 conjecture) claims that any positive integer
conjecture) claims that any positive integer  eventually returns to 1 when iterated through the following recursive formula
eventually returns to 1 when iterated through the following recursive formula  :
:
Contributed by: Alex Han (July 2015)
(Mathematica Summer Camp 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation