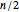Details

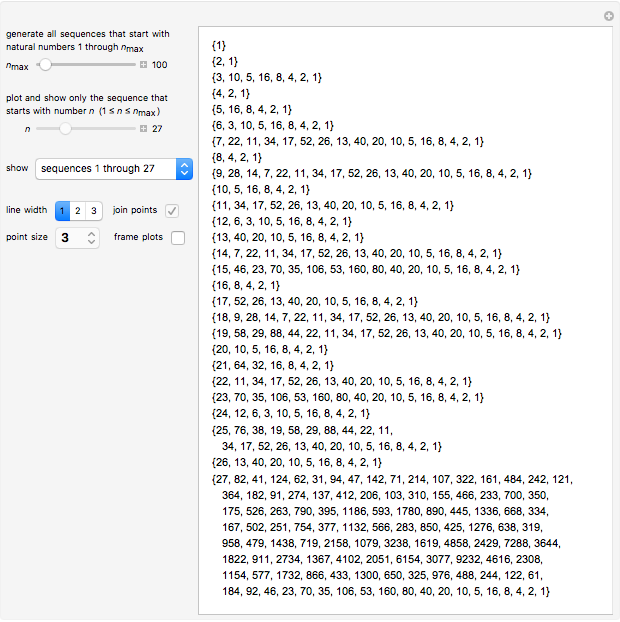
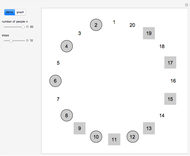
Snapshot 1: display of sequences starting with numbers 1 through 27

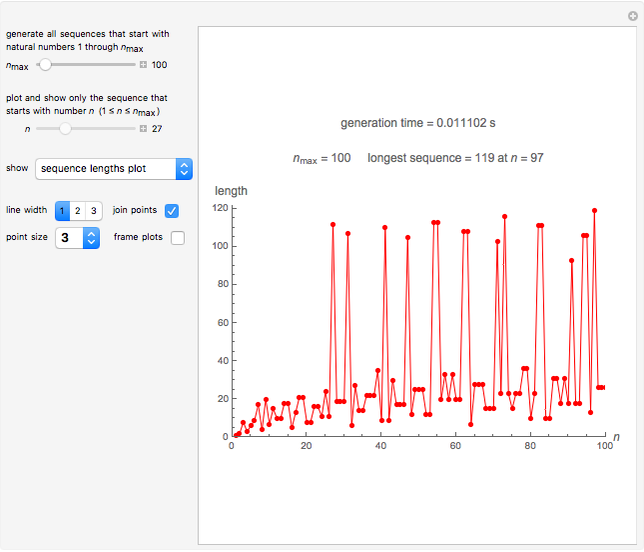
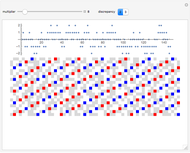
Snapshot 2: plot of the lengths of sequences starting with numbers 1 through 100; sequence 97 (i.e., the sequence starting with 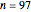) is the longest, having 119 values

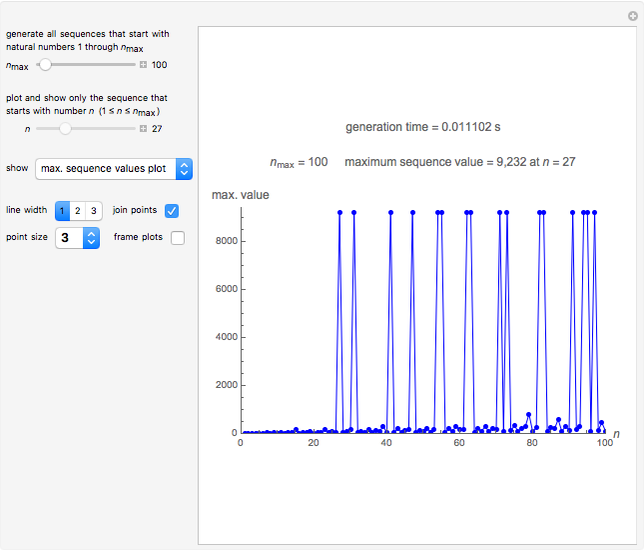
Snapshot 3: plot of the highest values in sequences starting with numbers 1 through 100; the global maximum 9232 occurs first in sequence 27

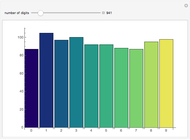
Snapshot 4: histogram of the lengths of sequences starting with numbers 1 through 100

Snapshot 5: histogram of the highest values that occur in sequences starting with numbers 1 through 100

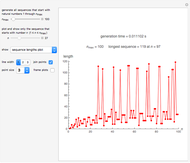
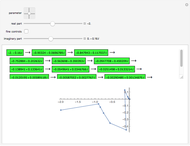
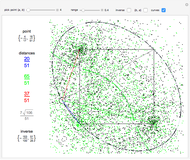
Snapshot 6: plot of the lengths of sequences starting with numbers 1 through 1500; sequence 1161 is longest and contains 182 values

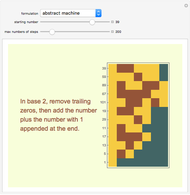
Snapshot 7: display and plot of sequence 1161, which has the longest length (182) of any sequence starting with numbers 1 through 1500

Snapshot 8: plot of the highest values in sequences starting with numbers 1 through 1500; five sequences share the maximum value of 250,504, which occurs first in sequence 703

Snapshot 9: plot and display of sequence 703, in which the highest value (250,504) first occurs in any of the sequences starting with numbers 1 through 1500 (see Snapshot 8)

Snapshot 10: histogram of the lengths of sequences starting with numbers 1 through 1500

Snapshot 11: histogram of the highest values in sequences starting with numbers 1 through 1500

Other names for the Collatz conjecture or problem [1] are: the or 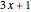[1, 3] conjecture or problem, the hailstone problem [1, 3, 4], Hasse's algorithm [1, 3], Kakutani's problem [1, 3], the Syracuse problem [1, 2, 3], Thwaites's conjecture [1], and Ulam's conjecture [1, 3].

The conjecture has, as of November 27, 2011, been shown to be true for all positive integers from 1 to 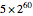(5,764,607,523,034,234,880) [1]. A counterexample would have to be either a periodic sequence that does not include 1 or a sequence that diverges to infinity [1].

The sequences of numbers generated are referred to as "hailstone" sequences or numbers [1, 3, 4] because their ascents and descents are reminiscent of the formation of hailstones in a cloud. They are also called "wondrous numbers" [1, 5]. The sequence's property of always returning to 1 has been called "oneness" [1].

The late Paul Erdős offered a $500 prize for solution of the Collatz conjecture [1, 6], and Sir Bryan Thwaites has offered a £1000 reward for the same.

Try setting 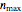to its largest value, 5000. In that case, the longest sequence starts at 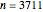and contains 238 values, as can be seen by choosing "sequence lengths plot" from the "show" popup menu. The highest sequence value is 8,153,620 when starting at 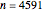, as can be seen by choosing "max. sequence values plot" from the "show" popup menu. You can see those sequences and their plots by setting the slider to either 3711 or 4591 and choosing "sequence and its plot" from the "show" popup menu.

Note that there is a noticeable delay (~5 seconds) when plotting either the "sequence lengths plot" or the "max. sequence values plot" for when "point size" is set to 1, 2, 4, or 5. For values of 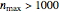, it is recommended to keep "point size" set to either 0 or 3 (indicated in boldface on the popup menu), in which case the plotting delay will be 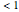second.

References

[1] Wikipedia. "Collatz Conjecture." (Nov 18, 2014) en.wikipedia.org/wiki/Collatz_conjecture.

[2] J. C. Lagarias, "The 3x + 1 Problem and Its Generalizations," The American Mathematical Monthly, 92(1), 1985 pp. 3–23. www.jstor.org/stable/2322189.

[3] C. D. Maddux and D. L. Johnson, Logo: A Retrospective, New York: Haworth Press, 1997 p. 160.

[4] C. A. Pickover, Wonders of Numbers, Oxford: Oxford University Press, 2001 pp. 116–118.

[5] D. R. Hofstadter, Gödel, Escher, Bach, New York: Basic Books, 1979 pp. 400–402.

[6] R. K. Guy, "Don't Try to Solve These Problems," The American Mathematical Monthly, 90(1), 1983 pp. 35–41. www.jstor.org/stable/2975688.