Von Neumann Regular Rings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
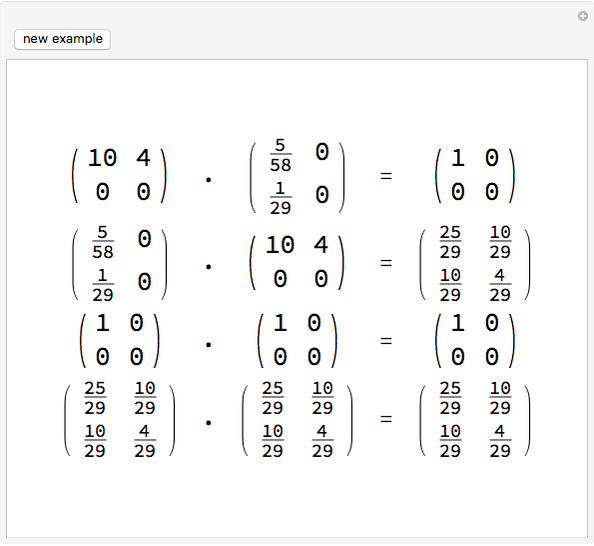
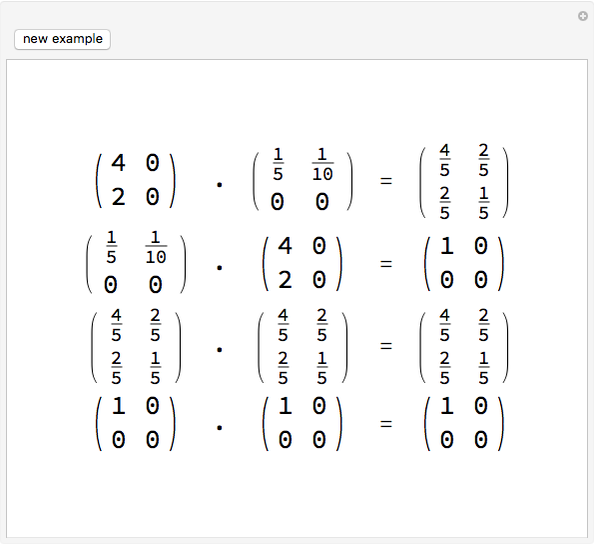
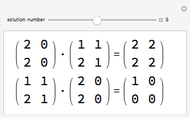
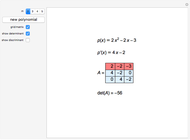
This Demonstration shows that the algebra of  matrices over the rational numbers is a von Neumann regular ring. A ring
matrices over the rational numbers is a von Neumann regular ring. A ring  is von Neumann regular provided that for every
is von Neumann regular provided that for every  there exists
there exists  such that
such that  . Every field is a regular ring, since
. Every field is a regular ring, since  , if
, if  . The simplest nontrivial example of a regular ring is an algebra of
. The simplest nontrivial example of a regular ring is an algebra of  matrices over some field. If
matrices over some field. If  , then
, then  , so
, so  is an idempotent in
is an idempotent in  . Similarly,
. Similarly,  is an idempotent. In Wolfram Mathematica, we get
is an idempotent. In Wolfram Mathematica, we get  from
from  by using the built-in PseudoInverse function.
by using the built-in PseudoInverse function.
Contributed by: Izidor Hafner (February 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
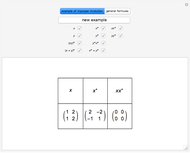
Nontrivial examples for  are matrices of rank 1. Obviously, nonzero matrices with one row or column of zeros are natural choices.
are matrices of rank 1. Obviously, nonzero matrices with one row or column of zeros are natural choices.
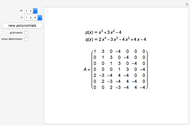
It can be shown that  matrices over a regular ring
matrices over a regular ring  form a regular ring [1, pp. 4–7].
form a regular ring [1, pp. 4–7].
Reference
[1] K. R. Goodearl, Von Neumann Regular Rings, San Francisco: Pitman, 1979.
Permanent Citation