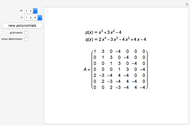
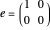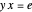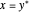Equivalence of Projections in Involutive Rings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Let  be a ring with involution
be a ring with involution  , that is,
, that is,  . An element
. An element 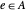 is called a projection if it is self-adjoint (
is called a projection if it is self-adjoint (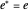 ) and idempotent (
) and idempotent ( ). The projections
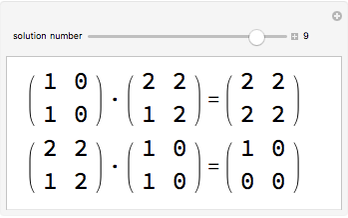
). The projections  and
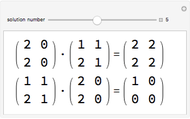
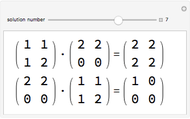
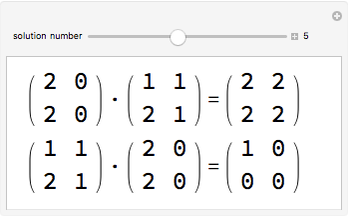
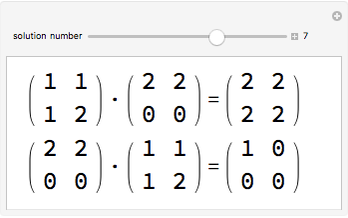
and  are said to be equivalent, written
are said to be equivalent, written  , when
, when 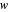 exists such that
exists such that  and
and 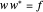 . Projections are algebraically equivalent if there exist
. Projections are algebraically equivalent if there exist  and
and  such that
such that  and
and  .
.
Contributed by: Izidor Hafner (March 2018)
Open content licensed under CC BY-NC-SA
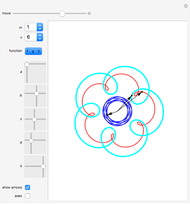
Snapshots
Details
This example and definitions were taken from [1, pp. 3–10].
References
[1] S. K. Berberian, Baer *-Rings, New York: Springer-Verlag 1972.
[2] I. Kaplansky, Rings of Operators, New York: W. A. Benjamin, 1968.
Permanent Citation