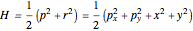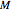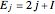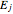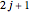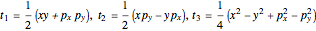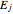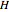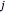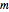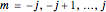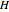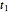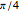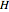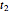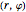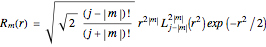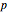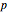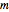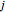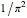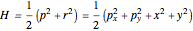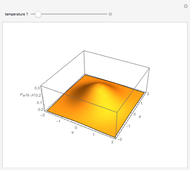
The two-dimensional isotropic harmonic oscillator is defined by the Hamiltonian
,
in units where the mass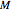
, the angular frequency
,
and Planck's constant
equal one. Its energy levels are
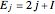, with
.
The degeneracy of the level associated with the energy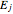
is also
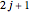. This remarkable degeneracy is due to the presence of three constants of the motion,
,
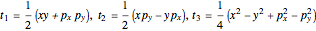which generate an SU(2)
algebra, just like three angular-momentum operators. The wavefunctions associated with an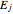
level may be taken to be simultaneous eigenfunctions of
and one of the
operators. The wavefunctions as well as the Wigner functions may accordingly be labeled by {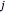
, 
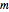} with
.
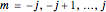Eigenfunctions common to
and
correspond to separation of the
and
variables. The case of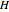
and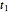
is completely analogous, but in a new coordinate system obtained by rotating the original one through an angle of
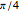. In both cases the wavefunctions and the Wigner functions are products of the corresponding one-dimensional quantities.
In this Demonstration we consider the less familiar common eigenstates of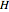
and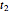
that correspond to a separation of variables in polar coordinates
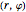. The wavefunctions are
, with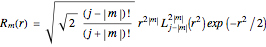
.
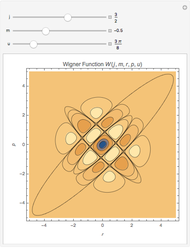
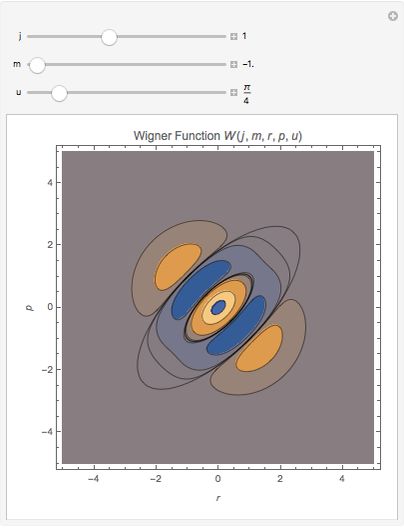
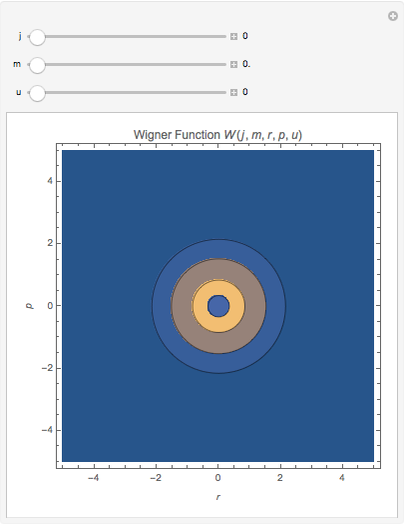
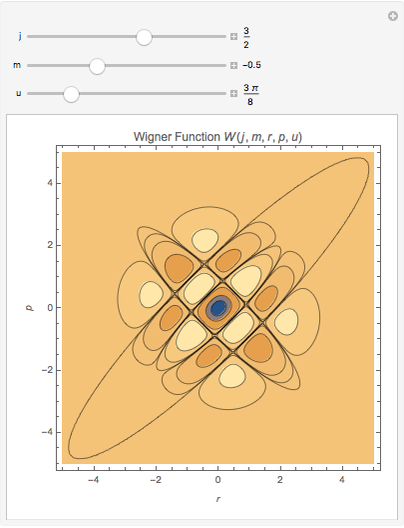
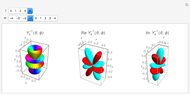
The corresponding Wigner functions have the form
.
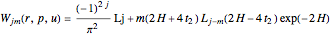They depend on the phase-space variables
,
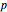, and
, where
and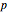
are the lengths of the
- and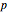
- vectors, and
is the angle between them. The variables enter through the functions
and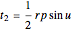
.
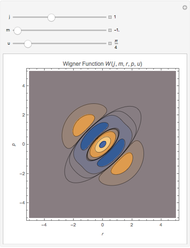
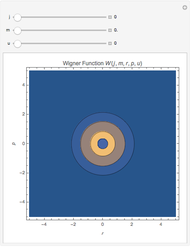
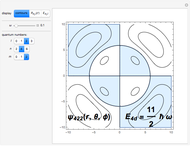
The Demonstration shows the dependence of the Wigner function on the quantum numbers
and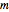
by means of contour plots. To see the dependence, move the
,
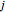, and
sliders. The contour values vary between
and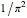
and become visible as you move the pointer across the contour lines.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
