The Kac Ring Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
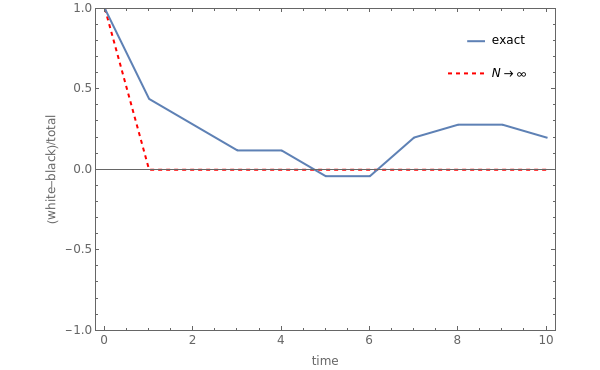
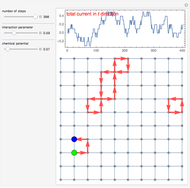
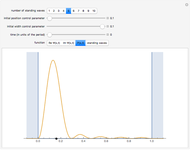
The Kac ring is a simple, explicitly solvable model that illustrates the process of passing from microscopic, time-reversible behavior to macroscopic, thermodynamic behavior [1]. In this model,  sites are arranged around a circle, forming a one-dimensional periodic lattice. Each site is occupied by either a black ball or a white ball. A fraction
sites are arranged around a circle, forming a one-dimensional periodic lattice. Each site is occupied by either a black ball or a white ball. A fraction  of the bonds joining neighboring sites have a "tunnel." From time
of the bonds joining neighboring sites have a "tunnel." From time  to time
to time  each ball moves to the clockwise neighboring site, changing its color if the ball crosses a tunnel.
each ball moves to the clockwise neighboring site, changing its color if the ball crosses a tunnel.
Contributed by: Daniel Díaz Simón and Andrés Santos (October 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In this model, a "microstate" at time  is characterized by
is characterized by  quantities: the color (black or white) of balls sitting on each of the sites. A "macrostate" at time
quantities: the color (black or white) of balls sitting on each of the sites. A "macrostate" at time  is characterized by a single coarse-grained quantity: the difference
is characterized by a single coarse-grained quantity: the difference  between the numbers of white and black balls, relative to the total number
between the numbers of white and black balls, relative to the total number  . The microscopic dynamics are reversible [2] and recurrent [3] (the microstate repeats itself after
. The microscopic dynamics are reversible [2] and recurrent [3] (the microstate repeats itself after  time steps). However, under a molecular chaos assumption (the fraction of white balls just about to cross a tunnel is assumed to be
time steps). However, under a molecular chaos assumption (the fraction of white balls just about to cross a tunnel is assumed to be  at any time) [4], the irreversible evolution equation
at any time) [4], the irreversible evolution equation  is expected to be correct in the limit
is expected to be correct in the limit 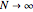 .
.
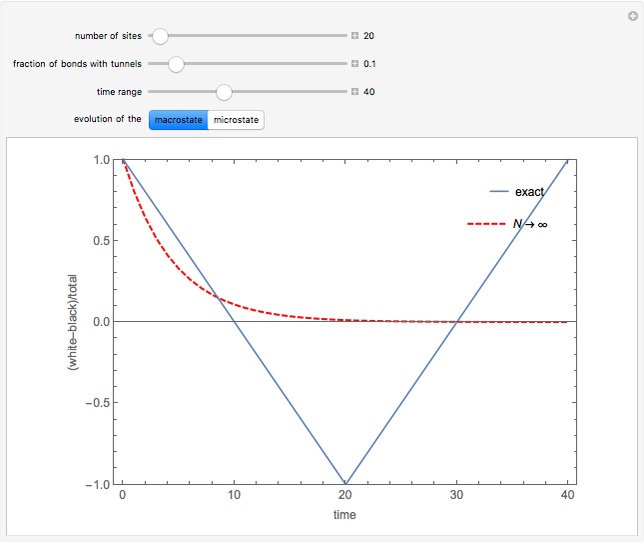
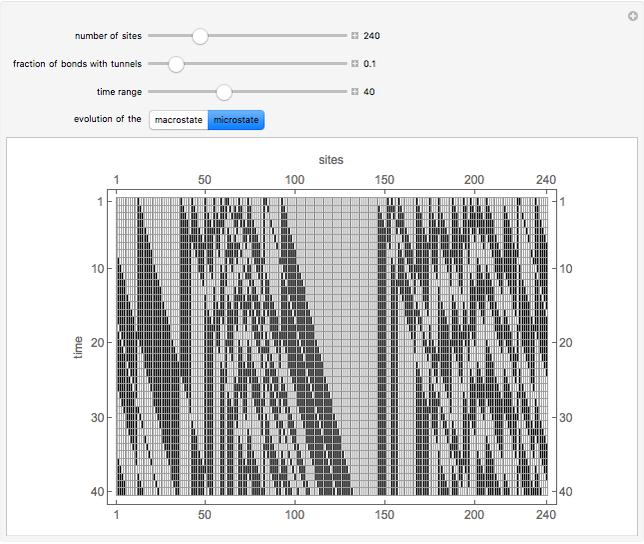
In this Demonstration, all the balls are white initially. You can control the total number of sites  , the fraction of bonds with a tunnel
, the fraction of bonds with a tunnel  and the time range to display. You can choose to follow the temporal evolution of the macrostate or the microstate.
and the time range to display. You can choose to follow the temporal evolution of the macrostate or the microstate.
References
[1] G. A. Gottwald and M. Oliver, "Boltzmann's Dilemma: An Introduction to Statistical Mechanics via the Kac Ring," SIAM Review, 51(3), 2009 pp. 613–635. doi:10.1137/070705799.
[2] Wikipedia. "Loschmidt's Paradox." (Oct 3, 2016) en.wikipedia.org/wiki/Loschmidt's_paradox.
[3] Wikipedia. "Poincaré Recurrence Theorem." (Oct 3, 2016) en.wikipedia.org/wiki/Poincaré_recurrence_theorem.
[4] Wikipedia. "Molecular Chaos." (Oct 3, 2016) en.wikipedia.org/wiki/Molecular_chaos.
Permanent Citation