Gillespie's Stochastic Simulation Algorithm for Chemical Reactions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
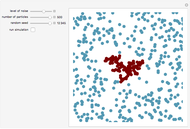
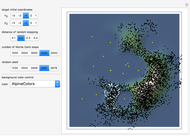
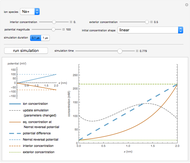
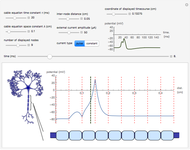
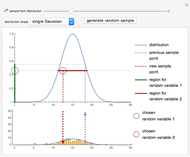
The Gillespie stochastic simulation algorithm is a Monte Carlo algorithm that simulates the time evolution of a chemical system according to its chemical master equation. In this Demonstration, the reaction 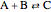 is simulated with variable forward
is simulated with variable forward 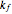 and backward
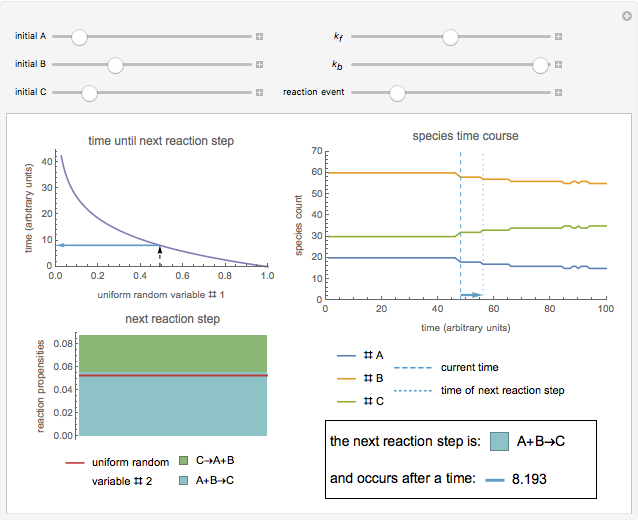
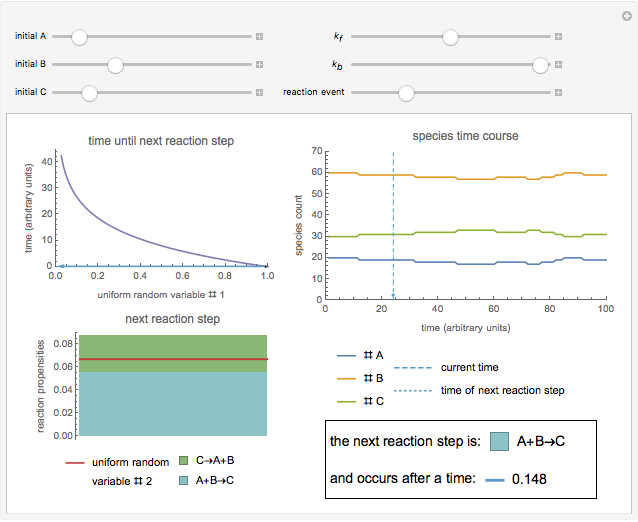
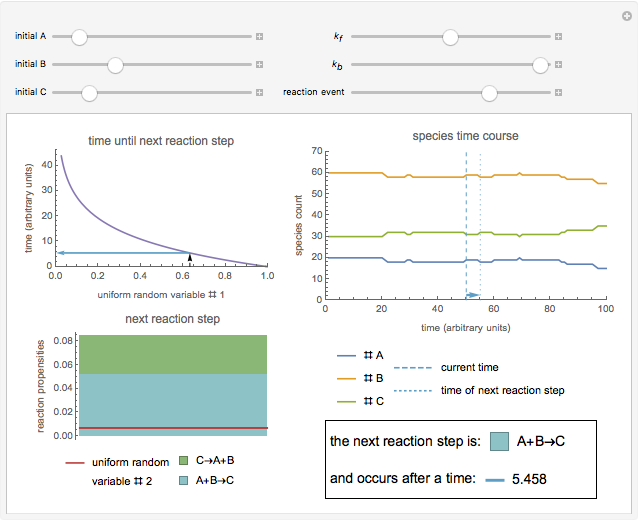
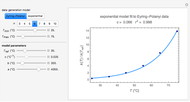
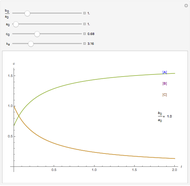
and backward 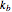 rate constants and initial particle numbers. The Demonstration shows the key steps of the Gillespie method. At the top left, the time until the next reaction is drawn from an exponential distribution. At the bottom left, the next reaction step (forward or backward) is randomly chosen based on the probabilities at each step of the reaction. The plot on the right shows the time course of each species
rate constants and initial particle numbers. The Demonstration shows the key steps of the Gillespie method. At the top left, the time until the next reaction is drawn from an exponential distribution. At the bottom left, the next reaction step (forward or backward) is randomly chosen based on the probabilities at each step of the reaction. The plot on the right shows the time course of each species 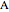 ,
, 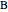 ,
,  . Use the "reaction event" slider to scroll in time through the reactions that occur.
. Use the "reaction event" slider to scroll in time through the reactions that occur.
Contributed by: Oliver K. Ernst (October 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: sample forward reaction step in the Gillespie algorithm
Snapshot 2: sample backward reaction step in the Gillespie algorithm
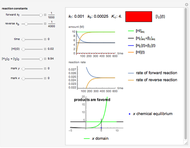
Snapshot 3: the reaction system tends toward equilibrium
The chemical master equation describes the time evolution of the probability distribution of possible states that describe the system. The Gillespie algorithm simulates a single trajectory of the state of the system, representing a sample from the probability distribution at each time point. In this Demonstration, the reaction 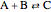 is considered to show the key steps of the algorithm. For further details on the Gillespie method, see [1, 2].
is considered to show the key steps of the algorithm. For further details on the Gillespie method, see [1, 2].
References
[1] D. Gillespie, "Exact Stochastic Simulation of Coupled Chemical Reactions," The Journal of Physical Chemistry, 81(25), 1977 pp. 2340–2361. doi:10.1021/j100540a008.
[2] D. Gillespie, "A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions," Journal of Computational Physics, 22(4), 1976 pp. 403–434. doi:10.1016/0021-9991(76)90041-3.
Permanent Citation