Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Discrete Fourier Sine and Cosine Transforms

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

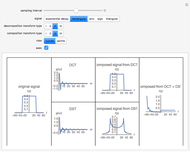
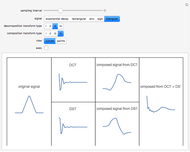
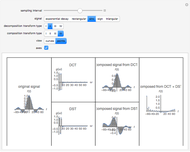
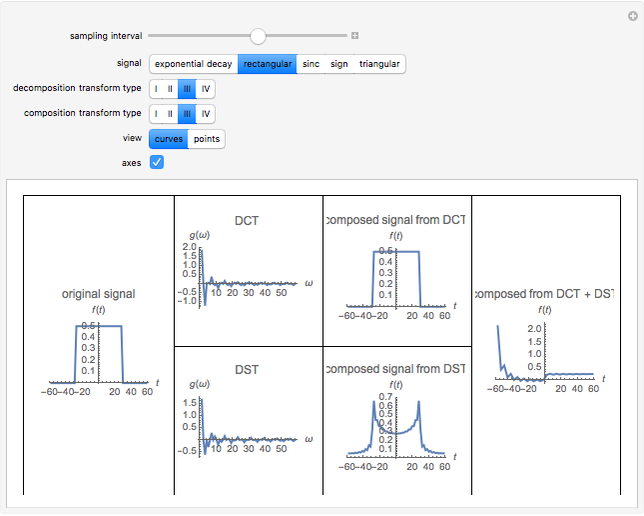
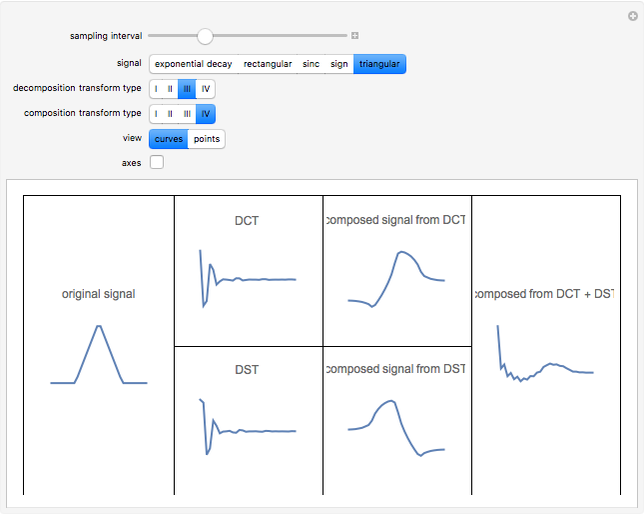
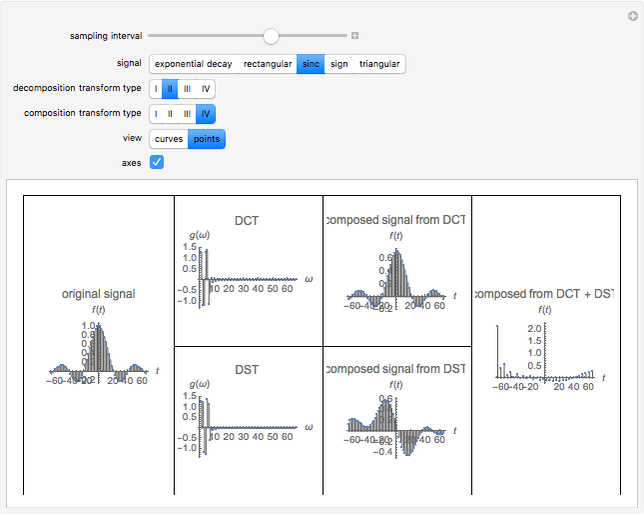
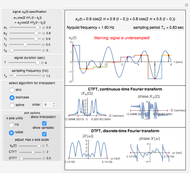
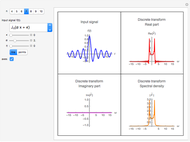
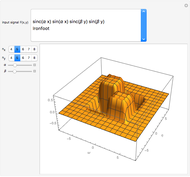
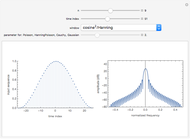
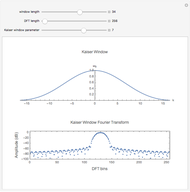
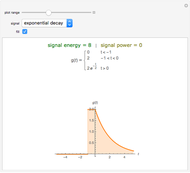
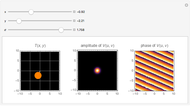
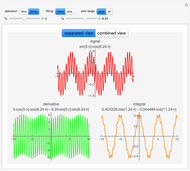
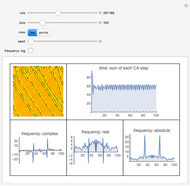
The discrete Fourier sine and cosine transforms (DST and DCT) can be used to decompose or represent a given digital signal (that is, discrete) in the form of a set of sums of sines and cosines. Four transform types are possible.

[more]

In the graphics, the initial signal is converted forward and back by the selected discrete Fourier transforms. For specific cases, either a cosine or a sine transform may be a better representation of the original signal than a combination of sine and cosine terms.

[less]

Contributed by: Daniel de Souza Carvalho (March 2011)
Aditional work by: Joe Bolte
Open content licensed under CC BY-NC-SA

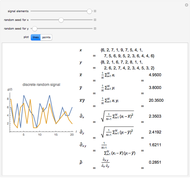
Snapshots

Details

The inverse transforms of types 1, 2, 3, and 4 are 1, 3, 2, and 4, respectively.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send