A Sliding Element in Rheological Models

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Mechanical analogs composed of springs and dashpots have been used extensively to describe qualitative and sometimes quantitative rheological properties of solids and liquids. However, there are deformation or flow patterns whose description requires additional elements. Among them is the sliding frictional or St. Venant element (see Details). This Demonstration represents these phenomena in simple arrays of force-displacement curves involving springs and/or dashpots.
Contributed by: Mark D. Normand and Micha Peleg (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The definition of the sliding (frictional or St. Venant) element is: if 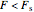 , then
, then  , else
, else  , where
, where  is the sliding force. Thus, in a series combination with a spring with spring constant
is the sliding force. Thus, in a series combination with a spring with spring constant  (model A), the array's constitutive definition is: if
(model A), the array's constitutive definition is: if  , then
, then  , else
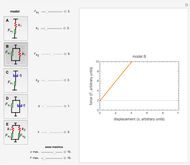
, else  . If the sliding element is parallel to the spring (model B), the array's definition is:
. If the sliding element is parallel to the spring (model B), the array's definition is:  . With a dashpot having viscosity
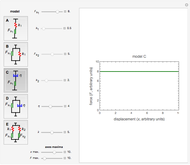
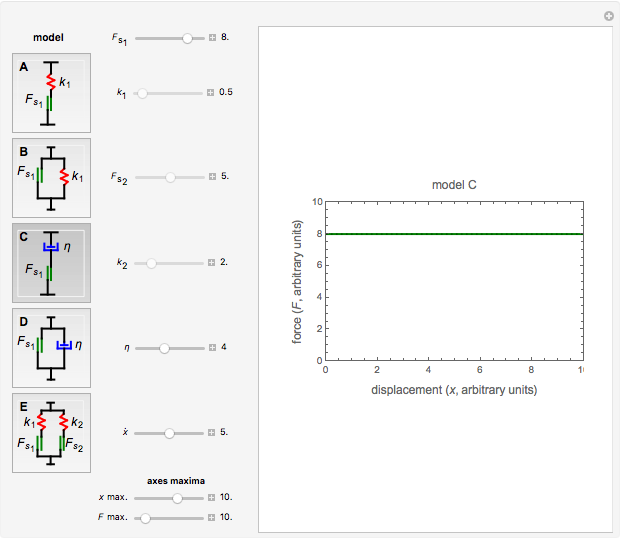
. With a dashpot having viscosity  in series (model C), the definition is: if
in series (model C), the definition is: if  , then
, then  , else
, else  , where
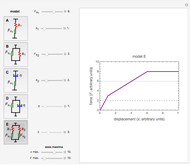
, where  is the displacement rate. With the dashpot in parallel (model D), the definition is:
is the displacement rate. With the dashpot in parallel (model D), the definition is:  . The definition of a model composed of two springs and sliders in series
. The definition of a model composed of two springs and sliders in series 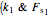 and
and  ) placed in parallel to each other (model E) is:
) placed in parallel to each other (model E) is:  if
if  , then
, then  , else
, else 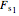 ) + (if
) + (if  , then
, then  , else
, else  ).
).
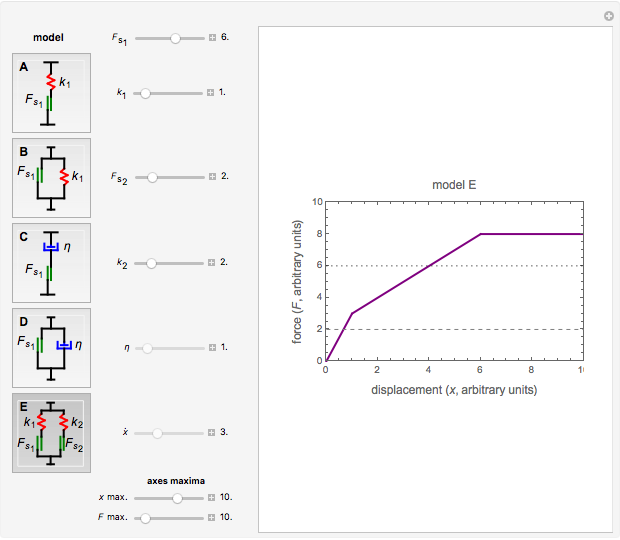
Choose model A, B, C, D or E by clicking its setter. You can set the magnitudes of 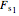 ,
,  ,
,  ,
,  ,
,  , and
, and  , all in arbitrary units, to plot the corresponding array's force-displacement curve. A horizontal dotted black line on the plot marks the magnitude of
, all in arbitrary units, to plot the corresponding array's force-displacement curve. A horizontal dotted black line on the plot marks the magnitude of 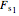 and a dashed gray line that of
and a dashed gray line that of  .
.
References
[1] J. L. White, Principles of Polymer Engineering Rheology, New York: John Wiley & Sons, 1990.
[2] N. S. Ottosen and M. Ristinmaa, The Mechanics of Constitutive Modeling, Amsterdam: Elsevier, 2005.
Permanent Citation