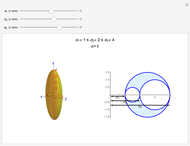
1. Ambiguous Rings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
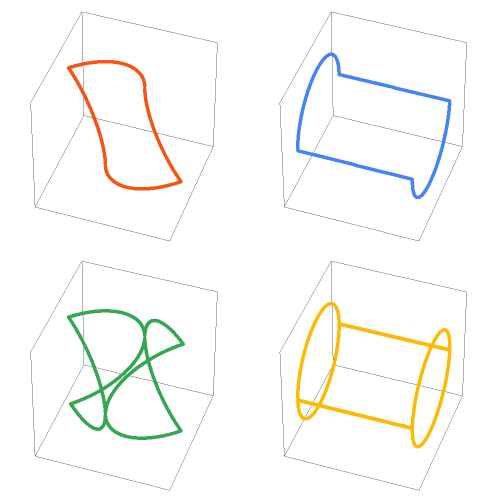
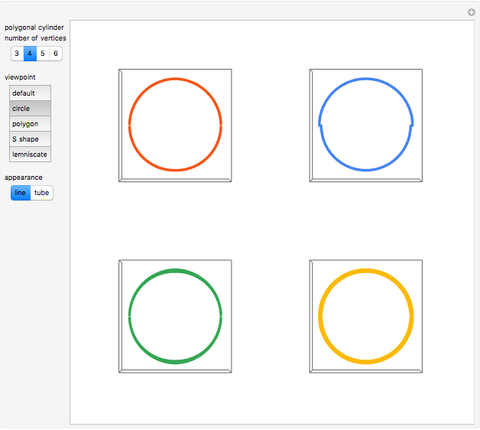
This Demonstration explores ambiguous rings.
[more]
Contributed by: Erik Mahieu (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The parametric equation of a circular cylinder with radius 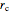 inclined at an angle
inclined at an angle  from the vertical is given by:
from the vertical is given by:
 ,
,
with parameters  and
and  .
.
Define the functions:
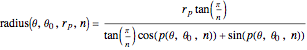

and
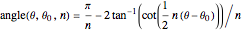 .
.
The 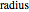 and
and 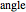 functions define the composite curve of the
functions define the composite curve of the  -gonal base of the polygonal cylinder [1].
-gonal base of the polygonal cylinder [1].
The parametric equation of a polygonal cylinder with  sides and radius
sides and radius 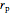 rotated by an angle
rotated by an angle 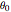 around its axis is given by:
around its axis is given by:
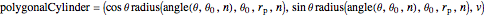 ,
,
with parameters  and
and  .
.
To find the equation of the intersection curve, set 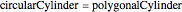 . This gives the three equations:
. This gives the three equations:
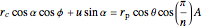 ,
,
 ,
,
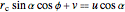 ,
,
with
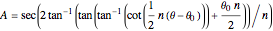 .
.
These are equations with four variables,  ,
,  ,
,  and
and  . Eliminating
. Eliminating  ,
,  and
and  by solving the equations gives the parametric equation of the intersection curve with
by solving the equations gives the parametric equation of the intersection curve with  as the only parameter:
as the only parameter:
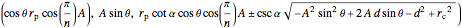 .
.
Reference
[1] E. Chicurel-Uziel, "Single Equation without Inequalities to Represent a Composite Curve," Computer Aided Geometric Design, 21(1), 2004 pp. 23–42. doi:10.1016/j.cagd.2003.07.011.
Permanent Citation