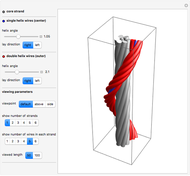
Planetary Gear Train

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
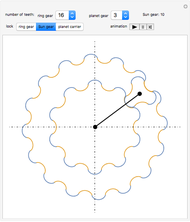
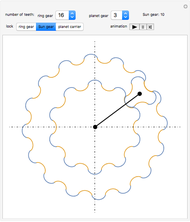
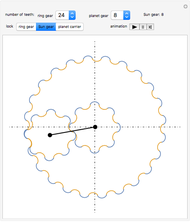
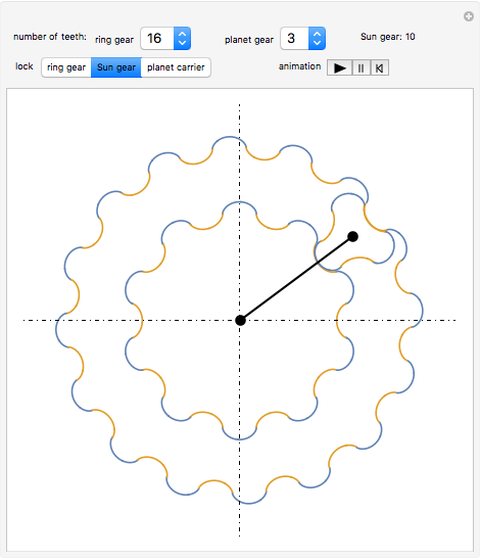
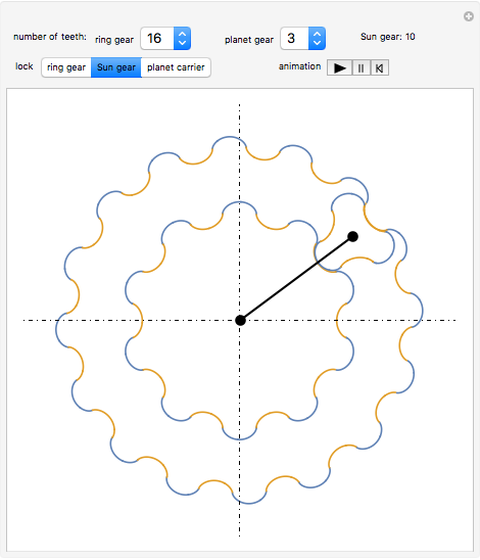
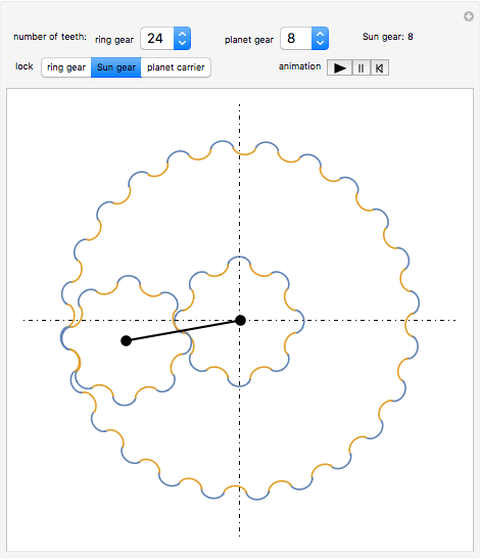
This Demonstration simulates a planetary gear train with cycloidal gears. A typical planetary gear train has three components: the ring gear, the Sun gear, and the planet carrier connecting the two together.
[more]
Contributed by: Erik Mahieu (March 2013)
Open content licensed under CC BY-NC-SA
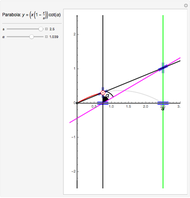
Snapshots
Details
Although a real world planetary gear train has three or four planet gears, for speed only one of these planet gears is shown.
For the gears to mesh, they need to have the same pitch. For cycloidal gears, this means that the radius has to be proportional to the number of teeth.
For the Sun and planet gears to fit within the ring gear, these geometric constraints are needed: 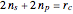 ,
, 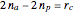 .
.
For the angular speeds of the gears to match, the following kinematic constraints are needed: 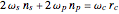 and
and 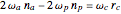 .
.
There are thus four equations in eight variables. In this Demonstration, 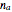 and
and  are inputs, and the system has two degrees of freedom. These are the combinations that you can choose:
are inputs, and the system has two degrees of freedom. These are the combinations that you can choose:
1. Lock the ring gear and drive the Sun gear (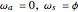 ).
).
2. Lock the Sun gear and drive the planet carrier (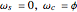 ).
).
3. Lock the planet carrier and drive the ring gear (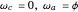 ).
).
Permanent Citation