Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Designs from Mechanical Linkages

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

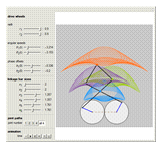
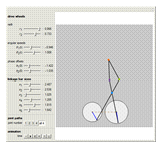
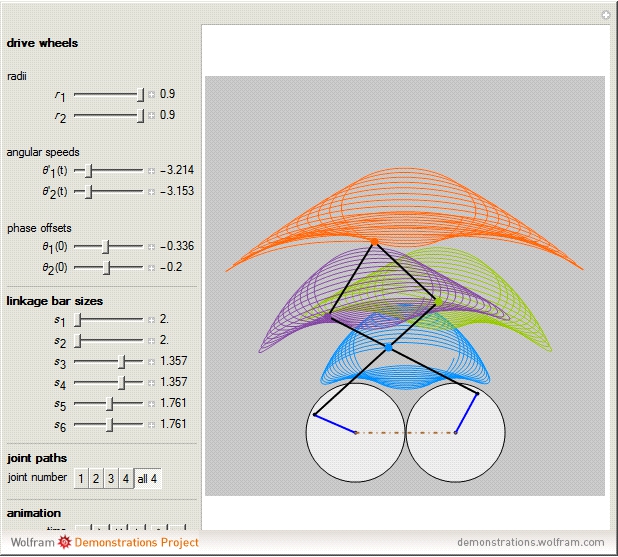
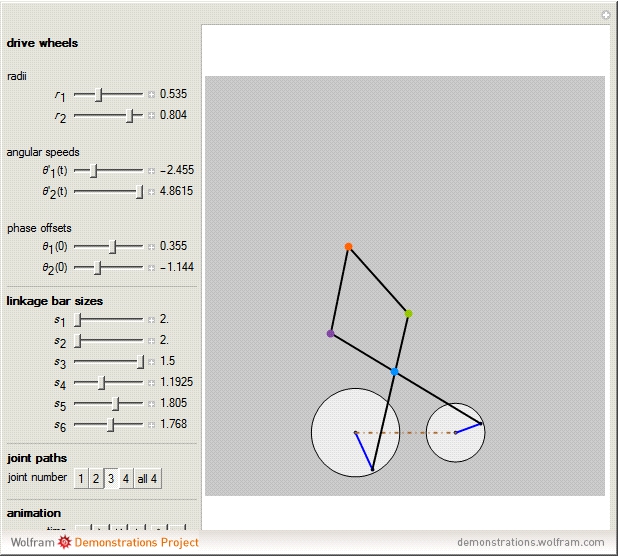
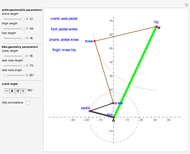
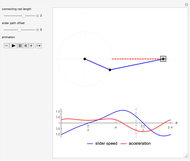
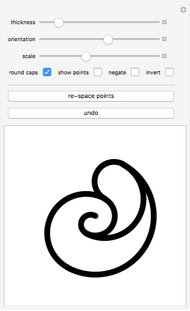
The paths of the joints of mechanical linkages have been used extensively to make all sorts of artistic designs: pantographs, pintographs, harmonographs, and so on.

[more]

The curve-drawing mechanism used in this Demonstration is a seven-bar linkage with six moving links and eight joints, resulting in two degrees of freedom according to the Grübler equation [1].

Changing the geometry of the linkage, but especially the angular speeds of the two wheels, generates a diverse range of curves.

[less]

Contributed by: Erik Mahieu (November 2015)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The Chebychev–Grübler–Kutzbach criterion states that 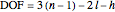, where in this Demonstration 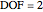is the number of degrees of freedom, is the number of links, is the number of joints, and is the number of ternary links. The two ternary links are the ones connecting three joints, and the remaining five links are binary links connecting two joints.

Reference

[1] Wikipedia."Chebychev–Grübler–Kutzbach Criterion." (Nov 17, 2015) en.wikipedia.org/wiki/Chebychev–Grübler–Kutzbach_criterion.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send