Intersection of a Generalized Cylinder over a Rose Curve with a Circular Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
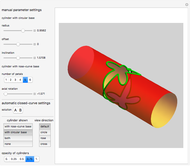
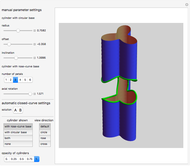
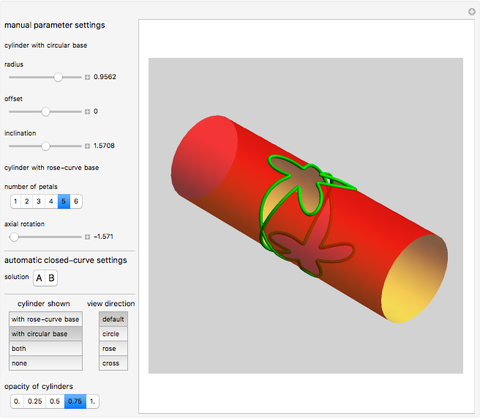
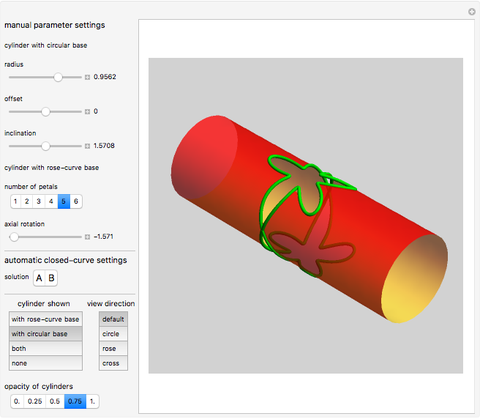
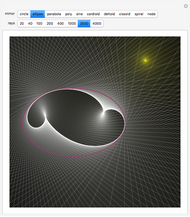
This Demonstration shows the intersections of a circular cylinder with a generalized cylinder over a rose curve with a variable number of petals.
[more]
Contributed by: Erik Mahieu (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The parametric equations of a circular cylinder with radius  , inclined at an angle
, inclined at an angle  and offset by a distance
and offset by a distance  from the horizontal are:
from the horizontal are:
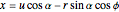 ,
,
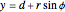 ,
,
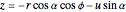 .
.
The parametric equations (with parameters  and
and  ) of a generalized upright cylinder over a rose curve in the
) of a generalized upright cylinder over a rose curve in the  -
-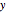 plane with
plane with  petals and an angular offset of
petals and an angular offset of 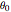 from the
from the  axis are:
axis are:
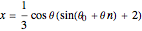 ,
,
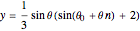 ,
,
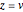 .
.
To find the intersection, set the corresponding equations equal to get three equations with four unknown parameters: 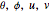 .
.
Eliminating all but  gives the two sections of the parametric of the composite intersection curve:
gives the two sections of the parametric of the composite intersection curve:

and
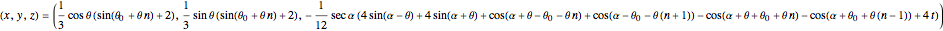
with
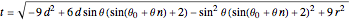 .
.
Reference
[1] E. Chicurel-Uziel, "Single Equation without Inequalities to Represent a Composite Curve," Computer Aided Geometric Design, 21(1), 2004 pp. 23–42. doi:10.1016/j.cagd.2003.07.011.
Permanent Citation