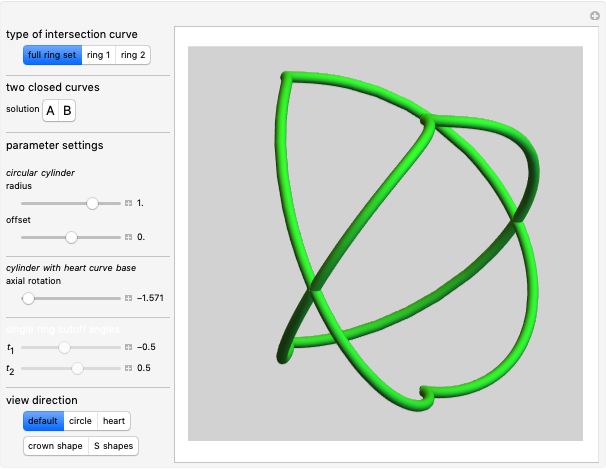
Noncircular Planetary Drive

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
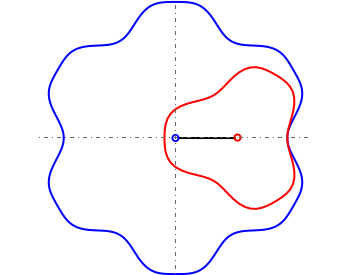
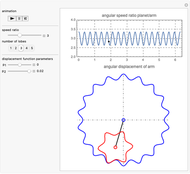
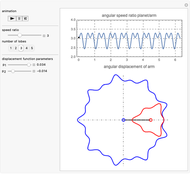
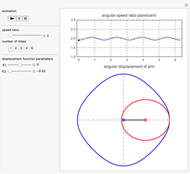
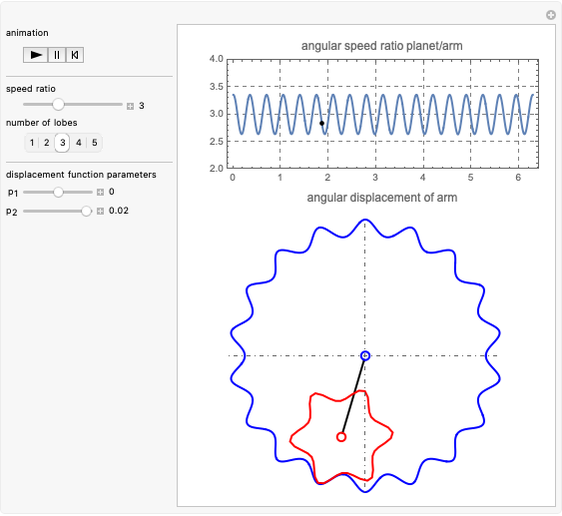
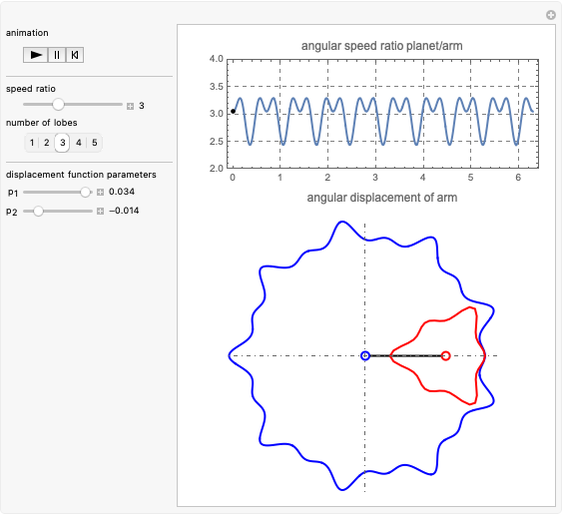
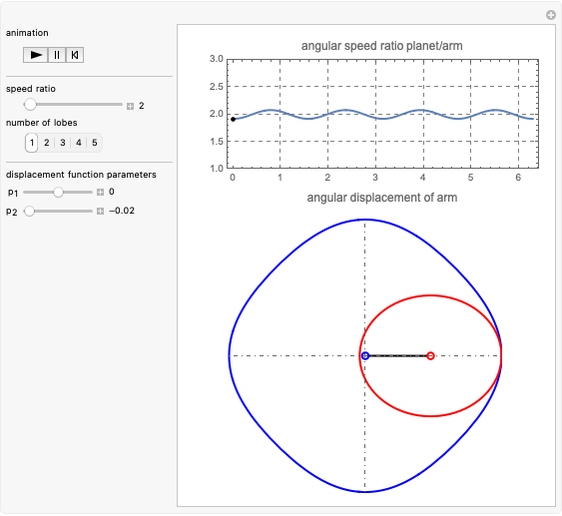
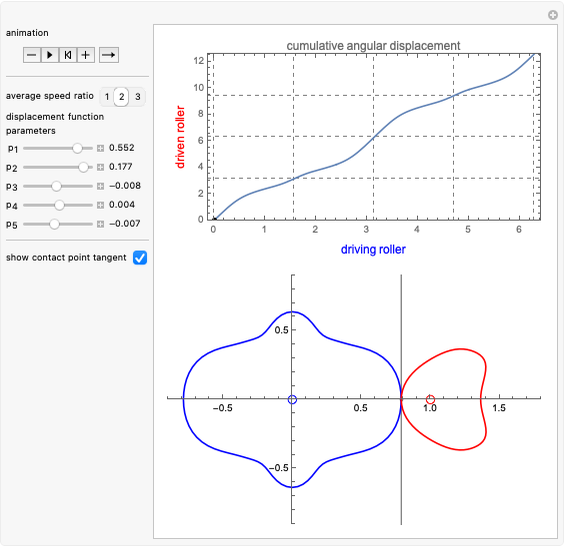
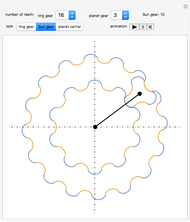
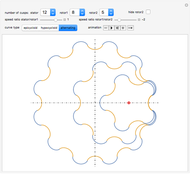
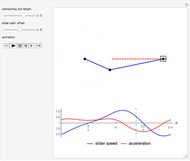
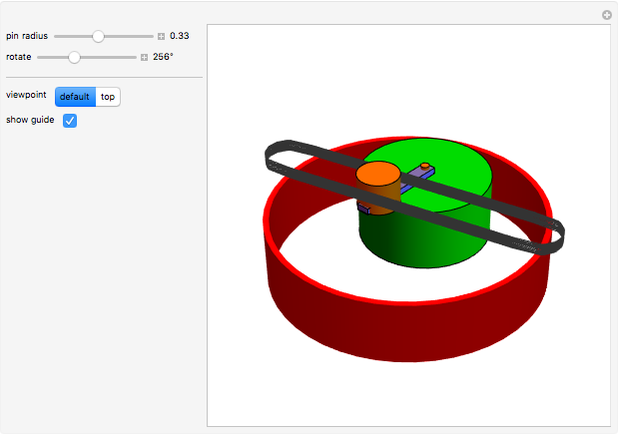
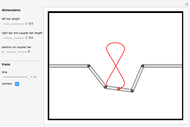
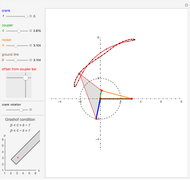
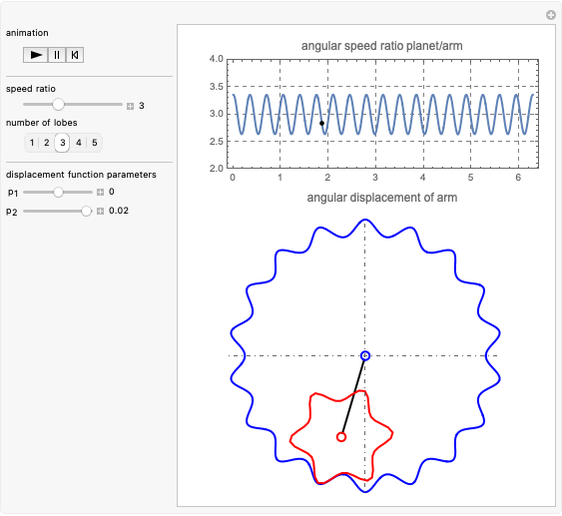
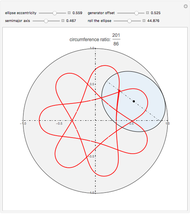
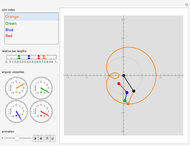
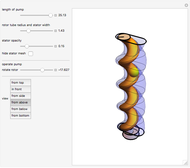
This Demonstration simulates a noncircular planetary roller drive by two curves (ring and planet), with the inside planet rolling without slipping.
[more]
Contributed by: Erik Mahieu (January 2014)
Open content licensed under CC BY-NC-SA
Details
The cumulative angular displacement function that generates the ring curve is given by 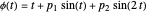 . The radii at the mutual contact point are
. The radii at the mutual contact point are 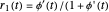 and
and 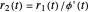 . These are effectively the polar equations of the two curves.
. These are effectively the polar equations of the two curves.
For a good article about noncircular gears, see [1].
Reference
[1] J. Doric, I. Klinar, and M. Dori, "One Approach for Modelling Intermittent Motion Mechanism with Noncircular Gears," Machine Design, 3(2), 2011 pp. 121–126. www.mdesign.ftn.uns.ac.rs/pdf/2011/no2/121-126.pdf.
Snapshots
Permanent Citation