2D and 3D Packard-Takens Autocorrelation Plots of Sinusoidal Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
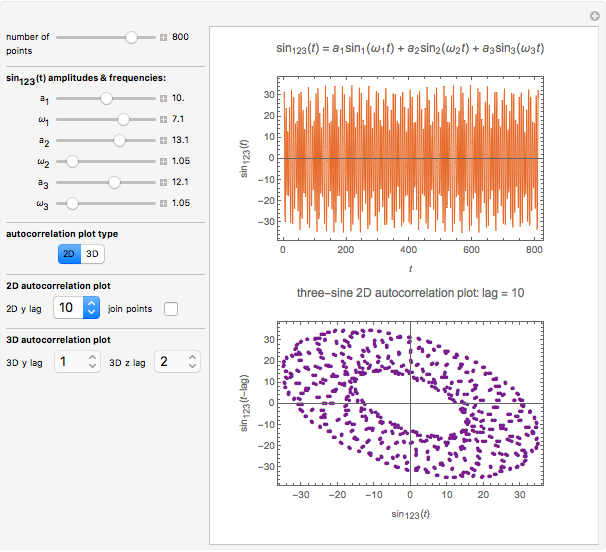
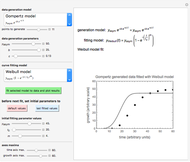
This Demonstration shows the autocorrelations of one- to three-term sinusoidal functions plotted in two and three dimensions. You can select the function's underlying amplitudes and frequencies as well as the lags and the number of generated points. You can also choose whether or not to connect the points in the two‐dimensional display only.
Contributed by: Mark D. Normand and Micha Peleg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
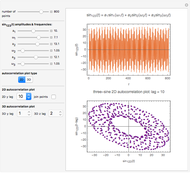
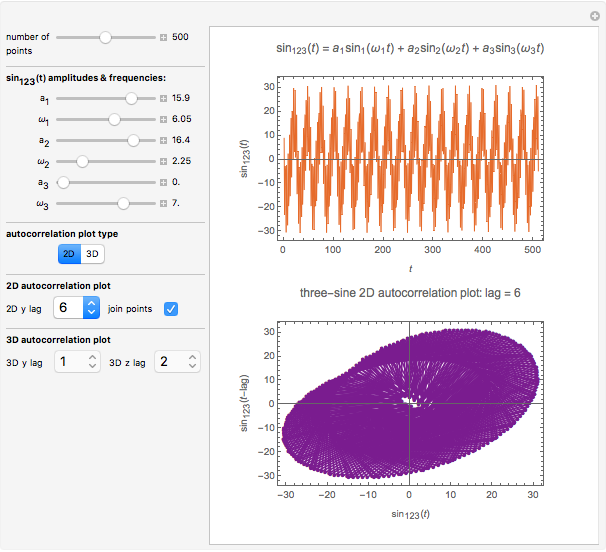
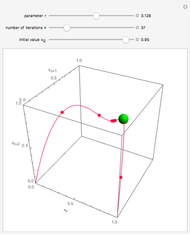
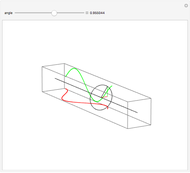
Snapshot 1: three-term sinusoidal function and its 2D autocorrelation plot with lag 10 and unconnected points
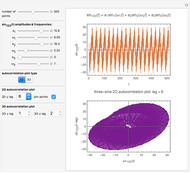
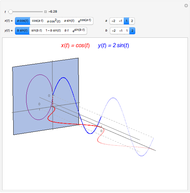
Snapshot 2: two-term sinusoidal function and its 2D autocorrelation plot with lag 6 and connected points
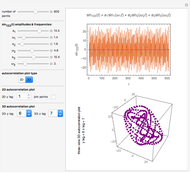
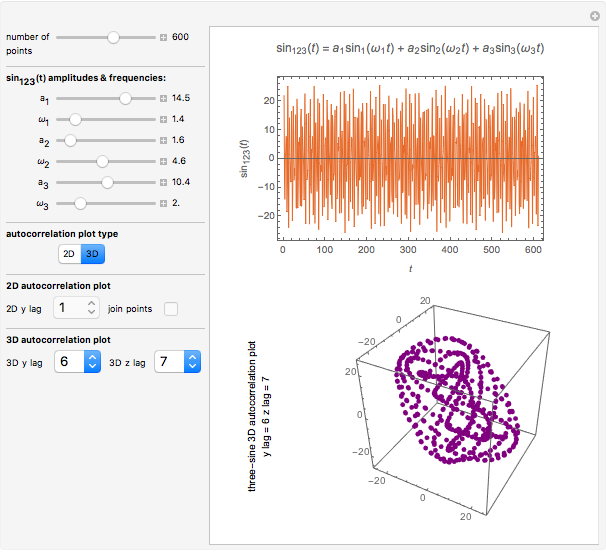
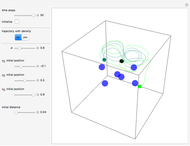
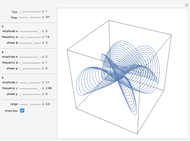
Snapshot 3: three-term sinusoidal function and its 3D autocorrelation plot with lags 6 and 7 and unconnected points
When a time series 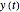 has underlying periodicities, a plot of
has underlying periodicities, a plot of 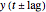 versus
versus 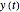 frequently yields an aesthetically appealing curve. The same is true for a three-dimensional display of
frequently yields an aesthetically appealing curve. The same is true for a three-dimensional display of 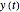 versus
versus 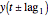 and
and 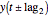 .
.
This Demonstration generates three-term sinusoidal functions and their corresponding Packard–Takens autocorrelation plots in two and three dimensions. You select the number of points to be generated, the function's underlying amplitudes, 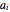 's, and frequencies,
's, and frequencies, 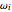 's, the lag for the 2D display and the two lags for the 3D display. An additional option is available to connect the points in the 2D display. The program then plots the selected sinusoidal function and the corresponding autocorrelation in the chosen display type.
's, the lag for the 2D display and the two lags for the 3D display. An additional option is available to connect the points in the 2D display. The program then plots the selected sinusoidal function and the corresponding autocorrelation in the chosen display type.
For functions having two sinusoidal terms, set either or both the 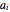 's or
's or 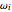 's to zero. For functions having only one sinusoidal term, set two
's to zero. For functions having only one sinusoidal term, set two 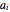 's and/or
's and/or 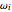 's to zero.
's to zero.
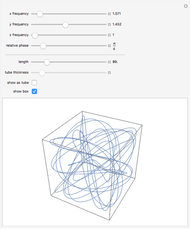
Notice that the 3D display may be viewed from different angles by clicking on the image and rotating it with the mouse. Tip: when searching for interesting autocorrelation patterns it is advisable to use a "number of points" setting that is low enough to maintain slider control responsiveness. The default setting of 250 or less is recommended. Once a pattern of interest has been found, the number of points may be increased and the points connected to reveal the pattern in more detail.
Reference: I. Stewart, Does God Play Dice?: The Mathematics of Chaos, Cambridge: Blackwell, 1989.
Permanent Citation