Wolfram Demonstrations Project

The 256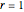

elementary cellular automata (ECA) rules can all be found somewhere among the four billion rules of the

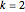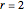cellular automata (CA). To find this correspondence, associate each three-bit neighborhood of the ECA with the four specific five-bit neighborhoods of the

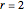CA that have the same three middle bits as the ECA. The resulting pattern is determined solely by the inner three bits, exactly like an

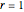rule. Essentially, the status of the outermost bits does not matter. But now, what about slight perturbations of this mapping? Will there be similarly shaped CA patterns or radically different patterns?

Contributed by: John Kiehl

Slider Zoom

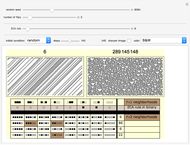
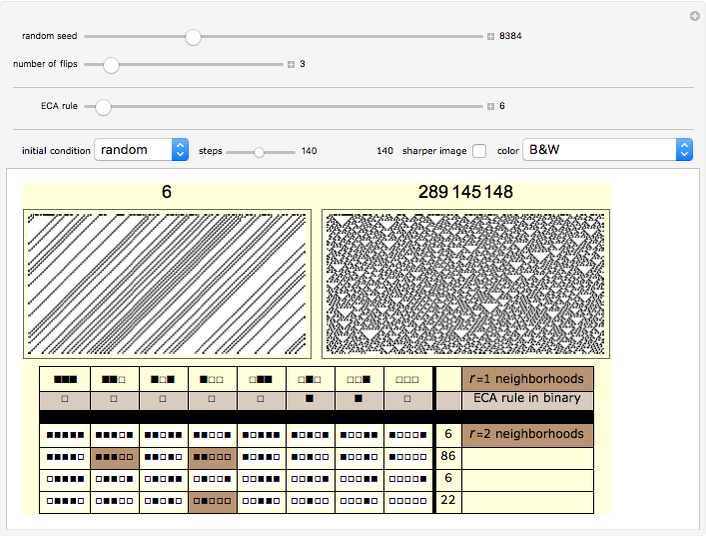
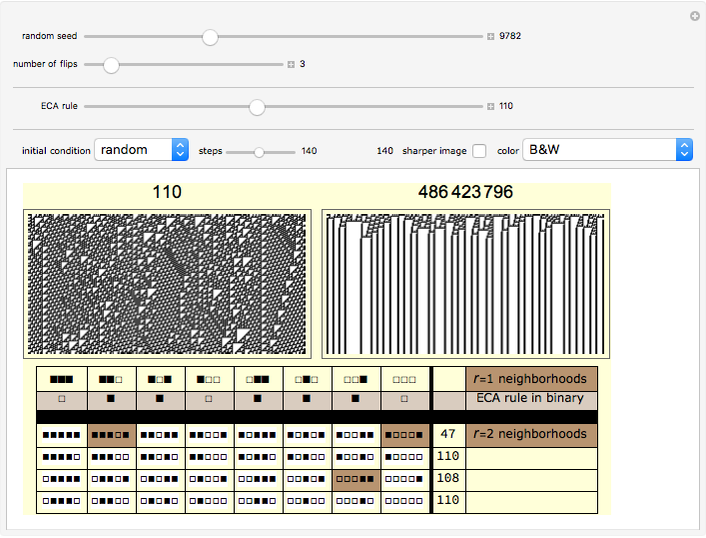
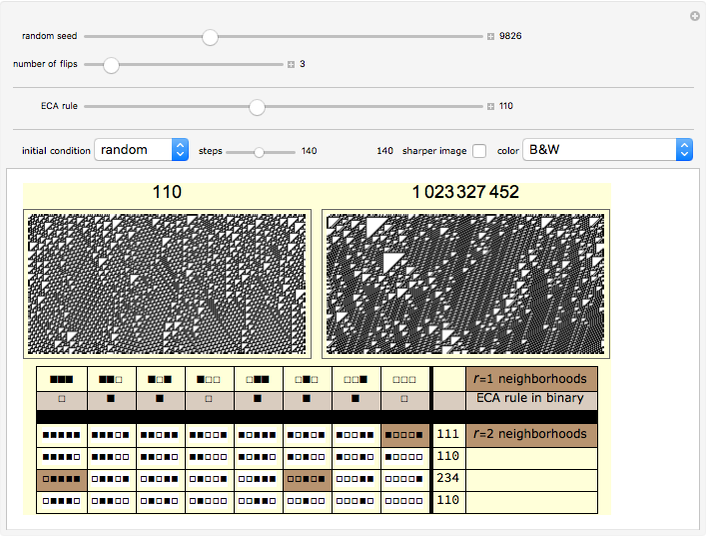
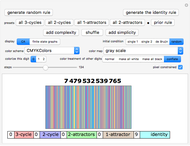
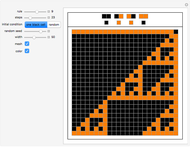
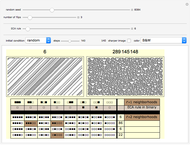
The lower left-hand side of the graphic above has eight columns—one column for each bit of the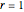

elementary cellular automata (ECA) rule. Below each bit of the ECA rule are the four neighborhoods of the larger

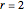rule space that have the same bit pattern for their middle three bits. If all four of these neighborhoods are assigned the same bit as the original bit of the ECA rule, the ECA is recreated in the

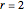rule space. This strategy essentially eliminates the influence of the outside bits on the unfolding pattern. In other words, the new

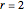rule's behavior is completely determined by the center bit and its two immediate neighbors, just like the

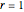rule.

The "number of flips" slider is initialized to zero to show you the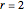

rule that exactly mimics the chosen ECA rule. Moving this slider will introduce bit flips, taking you to other

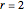rules that may or may not be similar in appearance. The flipped bits are highlighted in brown.

You can also click the 32 neighborhoods of the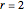

rule to flip the corresponding rule bit. These choices are highlighted in pink. In fact these mouse-chosen flips are not affected by the slider's choices, so the two strategies can be combined.

When the "number of flips" slider is set to "1", the "random seed" slider will sequentially step through all possible 32 bit flips. If you choose to flip two bits, there are 495 possible new combinations, and the random seed slider, again, will step through all the possibilities. For more than two bit flips the number of possibilities grows out of control, so the random seed slider will randomly select among the possible 32 bits. For example, there are 4960 ways to choose three bits from the 32 bits. The Mathematica command Binomial[32,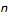

] will tell you how many different ways there are to choose

objects from a set of 32 objects where order does not matter.

It is helpful to hold the Option or Alt key while moving the "random seed" slider to allow it to change value more gradually.

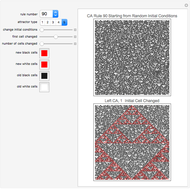
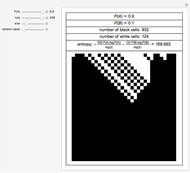
Snapshot 1: With only three bit flips this class 1 rule becomes class 4.

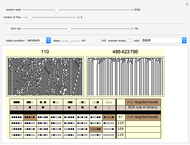
Snapshot 2: With three bit flips this class 4 rule becomes class 1.

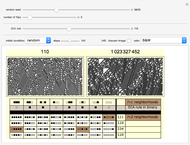
Snapshot 3: These three bit flips retain the class 4 behavior of ECA rule 110.

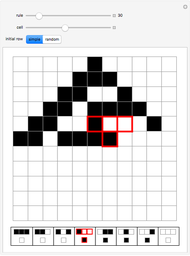
Snapshot 4: Here the bits are flipped by choosing specific neighborhoods with the mouse. These neighborhoods are highlighted in pink. Also, with "sharper image" unchecked you can zoom in or out using the "steps" slider.

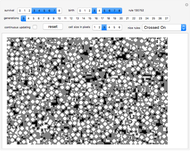
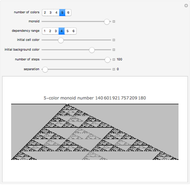
Snapshot 5: You can add color to the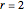

rule, which emphasizes local structures. See the Colorization of Cellular Automata Demonstration for other colorization strategies.

Snapshot 6: The five-bit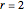

neighborhoods are arranged in four rows of eight neighborhoods. In each row the two outermost bits are the same. For example, in the first row the two outside bits are both black. Conceptually then you can think of each row as an eight-bit ECA rule embedded inside a particular bit pattern wrapper. The implied ECA rule is identified in the ninth column with its plot available as a tooltip.