Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

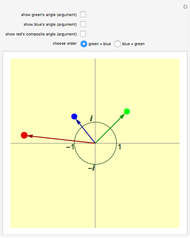
Root Routes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

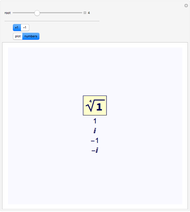
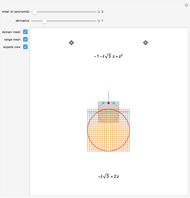
Historically, the search for the square root of minus one,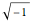, gave rise to the complex numbers. Typically we refer to as 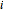. Perhaps the next obvious question is: what is 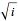? Do we need to invent another number, or can 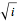be found in the complex plane?

[more]

The figure shows the complex number plane. The circle is the unit circle with -1 and labeled. As you drag the blue point, the red point shows you its squared value, that is, . So, of course, putting the blue point on puts the red point on -1. Where do you put the blue point to put the red point on ? Can you find a second solution? Don't forget every nonzero number has two square roots!

[less]

Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

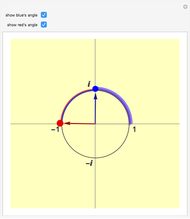
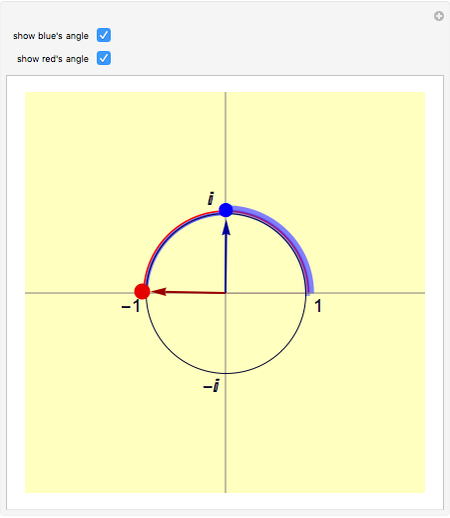
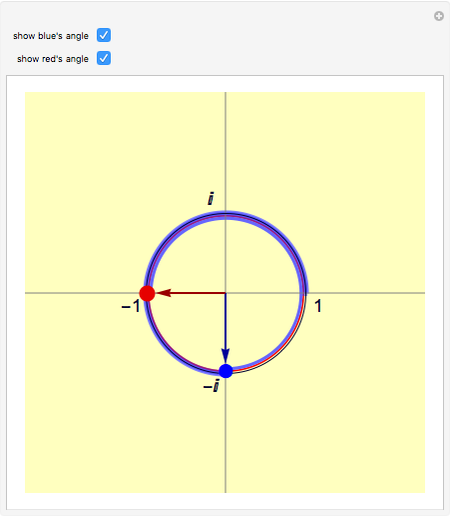
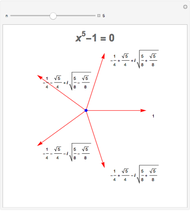
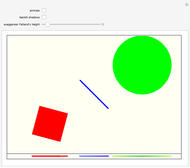
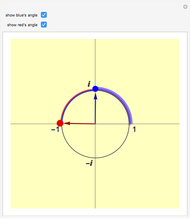
Snapshot 1: The blue point at 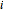is the square root of the red point at -1.

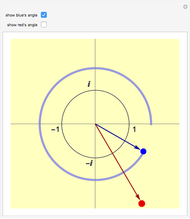
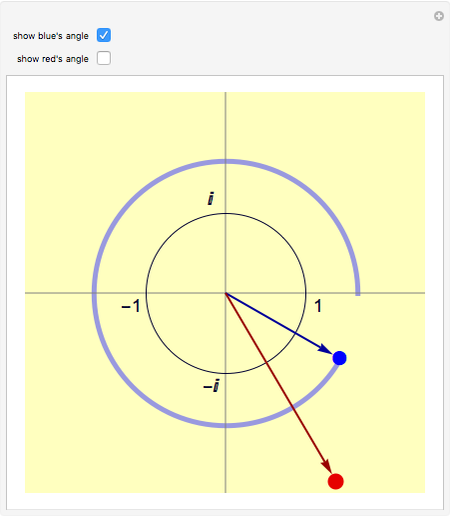
Snapshot 2: Here is the second square root of -1.

It is remarkable that only 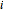is needed to allow you to take any root of any complex number to get a complex number. Even more: over the complexes, every polynomial equation has a solution.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send