Hysteresis Modeled with Cellular Automata

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
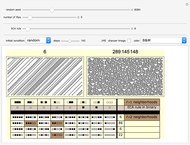
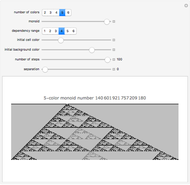
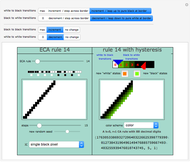
Hysteresis is the lagging of an effect behind its cause. This Demonstration models hysteresis using elementary cellular automata (ECA) by introducing additional color or gray shades that represent additional states as the cells transition between 0 and 1. You can choose the number of additional states by sliding the red and blue triangles in the upper right corner icon. The four toggler bars at the top further define the allowed transitions of the new colors.
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
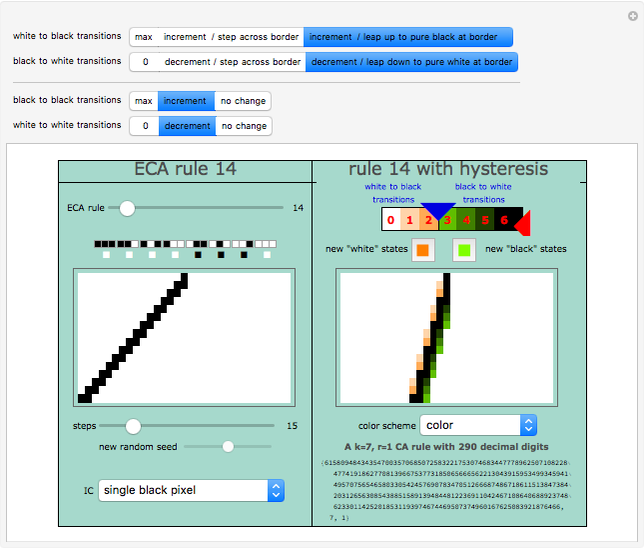
Snapshot 1: The 1 to 0 transitions experience hysteresis, while the 0 to 1 transitions remain the same as their ECA counterparts.
Snapshot 2: Hysteresis is introduced on the 0 to 1 transitions as well.
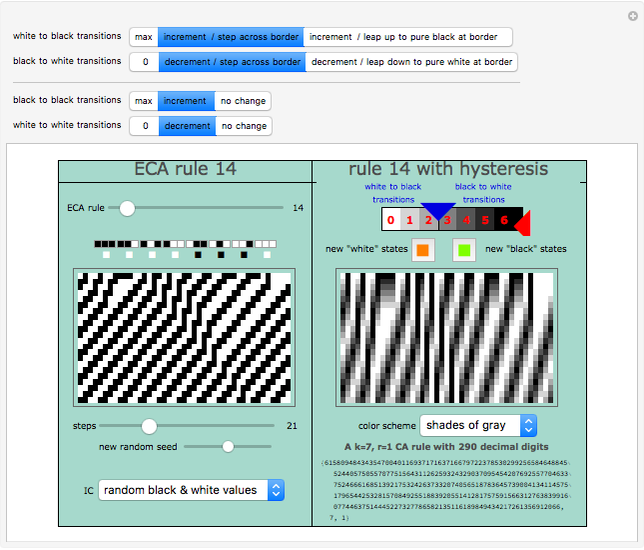
Snapshot 3: As specified by the toggler bars at the top, the new shades of gray incrementally drift among themselves rather than experiencing any instantaneous leaps to the extreme values of pure black or pure white.
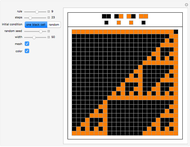
Snapshot 4: This color scheme maps all the new shades of gray back to their intended meaning of "white state" or "black state". This graphic is the heart of this Demonstration; that is, rule 14 has been morphed into another two-color rule by hysteresis.
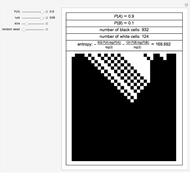
Snapshot 5: ECA Rule 30 loses its class 3 behavior because of hysteresis.
Snapshot 6: Rule 98, a class 2 ECA rule, appears to become class 3 because of hysteresis. A closer inspection is called for.
More discussion about the behavior of the gray shades in the higher- rule space:
rule space:
In general, the higher- rule space will have many shades of gray that correspond to the ECA rule's "0", and many shades of gray that correspond to the ECA rule's "1". What should it mean in the higher-
rule space will have many shades of gray that correspond to the ECA rule's "0", and many shades of gray that correspond to the ECA rule's "1". What should it mean in the higher- space to emulate the ECA's transition from 0 to 1, or 1 to 0, or for that matter to not transition (i.e., 0 remains 0, or 1 remains 1), since now there can be more than one value representing "0" or "1"? Simply stated, the basic strategy is that a 0 to 1 transition in the ECA should result in an increment in the higher-
space to emulate the ECA's transition from 0 to 1, or 1 to 0, or for that matter to not transition (i.e., 0 remains 0, or 1 remains 1), since now there can be more than one value representing "0" or "1"? Simply stated, the basic strategy is that a 0 to 1 transition in the ECA should result in an increment in the higher- space, while a 1 to 0 transition should result in a decrement.
space, while a 1 to 0 transition should result in a decrement.
There is a choice to be made at the border between the 0 region and the 1 region in the higher- rule space. For example, when a shade of gray in the 0 region borders on the 1 region, then a 0 to 1 transition could either result in the cell simply incrementing again—stepping across the border to the smallest 1 value—or, it could leap up to the maximum 1 value,
rule space. For example, when a shade of gray in the 0 region borders on the 1 region, then a 0 to 1 transition could either result in the cell simply incrementing again—stepping across the border to the smallest 1 value—or, it could leap up to the maximum 1 value,  , represented by black. This is what is meant by the phrases "step across border" or "leap up to pure black at border" in the toggler bars at the top.
, represented by black. This is what is meant by the phrases "step across border" or "leap up to pure black at border" in the toggler bars at the top.
In a non-transition like 0 remaining 0 in the ECA, a slightly different question arises in the higher- space. Should the relevant, new gray cells remain constant, decrement toward zero, or jump immediately all the way back to zero? Similarly, in a 1 to 1 non-transition should the relevant gray cells remain constant, increment toward the maximum value, or jump immediately up to the maximum value? The top two toggler bar controls at the top are provided to specify and explore these variations.
space. Should the relevant, new gray cells remain constant, decrement toward zero, or jump immediately all the way back to zero? Similarly, in a 1 to 1 non-transition should the relevant gray cells remain constant, increment toward the maximum value, or jump immediately up to the maximum value? The top two toggler bar controls at the top are provided to specify and explore these variations.
In all cases, the new shades of gray, when viewed as neighbor cells, behave simply as a "one" or a "zero". If their graduated gray values were somehow incorporated into the algorithms for rule transitions, a "continuous CA" would have been created, which was not the intention of this Demonstration. The goal here is to simply explore the notion of a different gradient when transitioning between 0 and 1 versus transitioning between 1 and 0.
An interesting "reverse problem" implied by this Demonstration is: can you recognize, a priori, when a rule in a  rule space is, in fact, a trivial elaboration of an ECA rule?
rule space is, in fact, a trivial elaboration of an ECA rule?
Permanent Citation