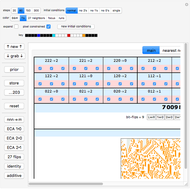
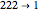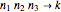Stepping through k=3, r=1 Cellular Automata Rule Space

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
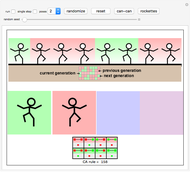
The 3-color, nearest-neighbor, one-dimensional (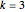 ,
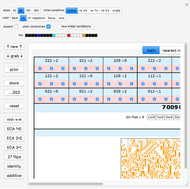
, 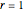 ) cellular automaton (CA) rule space has over seven trillion rules. In this Demonstration you can restrict your exploration to a subset of this rule space by using the checkboxes in the pink regions. Click the "↑ new ↑" button to choose a rule at random from your constructed subspace.
) cellular automaton (CA) rule space has over seven trillion rules. In this Demonstration you can restrict your exploration to a subset of this rule space by using the checkboxes in the pink regions. Click the "↑ new ↑" button to choose a rule at random from your constructed subspace.
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Quick Start
Click "reset" to make the entire rule space available. Click "↑ new ↑" repeatedly until you find a rule that interests you. Select the "nearest neighbors" tab. Click any thumbnail within that tab that now appeals to you. Click "nnn → m" to create a small, 27-rule subspace. Select the "entire subspace" tab. Click any thumbnail that interests you here. Continue to revisit the "nearest neighbors" and "entire subspace" tabs to find new, interesting rules.
Overview
This Demonstration implements two strategies to explore the vast 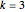 ,
, 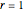 rule space. The first strategy, pursued in the "nearest neighbors" tab, finds the 54 rules that differ from the current rule by just a single digit in its base-three representation. Typically, these rules resemble the original rule, but some rules display dramatically different behavior. Clicking any of these thumbnails makes that rule the current rule and returns you to the main tab for a closer look. This makes a new set of nearest neighbors become available for this rule in the "nearest neighbors" tab. And so, your stepwise, incremental journey through the rule space is underway.
rule space. The first strategy, pursued in the "nearest neighbors" tab, finds the 54 rules that differ from the current rule by just a single digit in its base-three representation. Typically, these rules resemble the original rule, but some rules display dramatically different behavior. Clicking any of these thumbnails makes that rule the current rule and returns you to the main tab for a closer look. This makes a new set of nearest neighbors become available for this rule in the "nearest neighbors" tab. And so, your stepwise, incremental journey through the rule space is underway.
The second strategy, implemented by the 81 checkboxes in the "main" tab and pursued in the "entire subspace" tab, lets you define a more general subset of rules than the first strategy. In this strategy you determine which of the 27 neighborhoods are allowed to transition to new states and which neighborhoods are constrained to remain constant. To get started you could set the checkboxes to correspond to the current rule by clicking the "↓ grab ↓" button, and then check a handful of additional checkboxes to build a subspace. By visiting the "entire subspace" tab, you would survey this subspace and choose a new rule on which to focus.
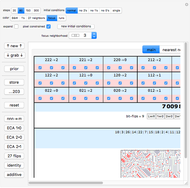
"main" tab
Use the checkboxes to create a range of rules to explore. A 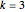 ,
, 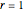 rule can be defined by the transitions of 27 input neighborhoods, so here each one of the 27 neighborhoods has three checkboxes that represent the three possible states (2, 1, 0, left to right) which that neighborhood can transition to.
rule can be defined by the transitions of 27 input neighborhoods, so here each one of the 27 neighborhoods has three checkboxes that represent the three possible states (2, 1, 0, left to right) which that neighborhood can transition to.
Click the "↑ new ↑" button to choose randomly from your specified rule subspace. The arrows in the "↑ new ↑" button hint at the direction of the flow of information, which is from the checkbox regions up into the light-blue rule specification regions.
The "↓ grab ↓" button works in reverse: it sets the checkboxes by bringing down the specification of the current rule in the light-blue region into the checkbox region. It is assumed that you would vary or add to this setting before clicking "↑ new ↑" again. As a matter of fact, the "↑ new ↑" button is disabled after checking "↓ grab ↓" until you augment or change the checkboxes. For example, clicking the "nnn → m" preset after clicking the "↓ grab ↓" button creates a manageable 27-rule subspace; or, for example, clicking the "ECA 1•0" button after clicking the "↓ grab ↓" button creates a 256 rule subspace that surrounds the 256 elementary cellular automaton (ECA) rules with the current state of the 19 neighborhoods that contain the digit 2.
When two or more checkboxes are checked for any one neighborhood, they are highlighted in pink. A subspace is generated only when at least one neighborhood has a pink background.
The size of your current subspace is shown below the rule number.
To the left of the subspace size notification are five push buttons that let you access the 11 rules that are symmetrically equivalent to the current rule. For example, the "2 ↔ 0" push button exchanges the black and white pixels that are represented by the 2 and 0 digits; the "(012)" button permutes the color scheme by sending 0 to 1, 1 to 2, and 2 to 0; and the "L ↔ R" button forces a mirror reflection without changing the color scheme.
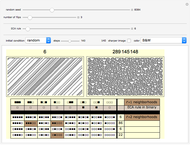
The 27 base-three digits that encode each rule are arranged in three rows of nine. Notice the top row has the digit 2 as the left neighbor, the middle row has 1 as the left neighbor, and the bottom row has 0 as the left neighbor. The right neighbors cycle through the nine columns, 2, 1, 0, respectively. All the neighborhoods with 2 as the center digit are found in the three left-most columns; the neighborhoods with 0 as a center digit are found in the right-most columns, and those with 1 as a center digit are found in the center columns. Rod Obando coined the term "primitives" to refer to the neighborhoods with the same center digit. Rod suggests keeping track of which bits are stabilized by a rule's specification versus which bits are flipping to other values. The quantity of bits that flip is displayed underneath the rule number. It is very difficult to find chaotic rules that have less than nine rule bits flipping, but not impossible. See the bookmarks for some low-flipping examples. Equally fascinating is finding nonchaotic, class-2 rules that have all 27 neighborhoods flipping. Both the "nearest neighbor" and "entire subspace" display their thumbnails with color-coded backgrounds that indicate when a new rule would have less flips than the current rule. See the discussion on those tabs below.
Some rules behave differently if the initial conditions lack one of the three digits, hence the alternate initial condition choices. The author has found rules with as few as four neighborhoods flipping that exhibit long-term chaotic behavior if the initial condition is devoid of a certain digit. These rules are archived in the bookmarks.
The "single" initial condition creates the six possible variations of the three digits surrounded by a sea of their complement digits. It is best viewed with 150 steps.
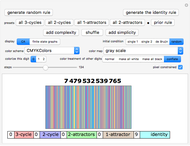
If a rule has the potential to emulate a 2-color, elementary cellular automaton (ECA) rule, a comment identifies the specific ECA rule. Furthermore, the comment explains which two of the three 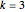 ,
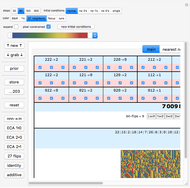
, 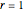 rule colors are involved. The ECA behavior is often constrained between columns of vertical structures that incorporate the third color. Click "identity" to see an extreme example of this. A logical strategy to follow after discovering one of these rules would be to click one of the "ECA …" presets on the left, and then view the 256 variations in the "entire subspace" tab.
rule colors are involved. The ECA behavior is often constrained between columns of vertical structures that incorporate the third color. Click "identity" to see an extreme example of this. A logical strategy to follow after discovering one of these rules would be to click one of the "ECA …" presets on the left, and then view the 256 variations in the "entire subspace" tab.
Coloring
Various coloring schemes are available.
B&W: the canonical black, gray, white scheme
1's: consecutive, vertical runs of 1-digits are colored one of four colors determined by the digit that precedes and follows the run. A reminder key pops up in this mode:
— (2 11…11 2) is blue — (2 11…11 0) is cyan — (0 11…11 0) is red — (0 11…11 2) is orange
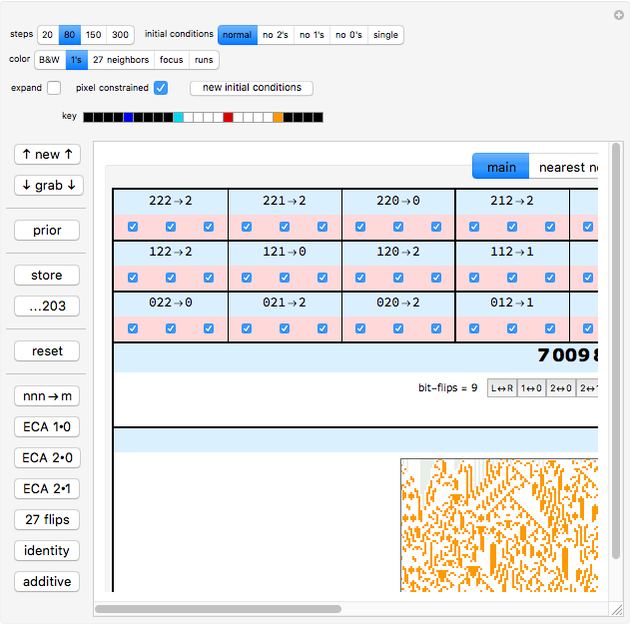
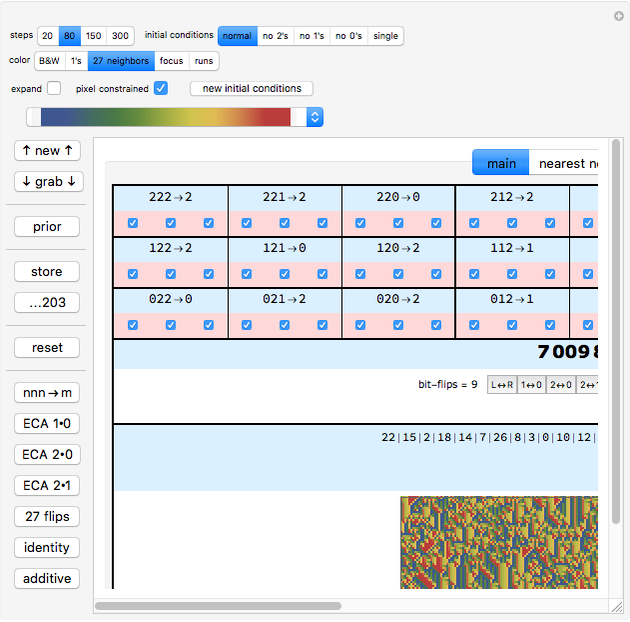
27 neighbors: a specific color is assigned to each pixel based on that pixel's 3-digit neighborhood. A dropdown menu allows you to choose between various color schemes.
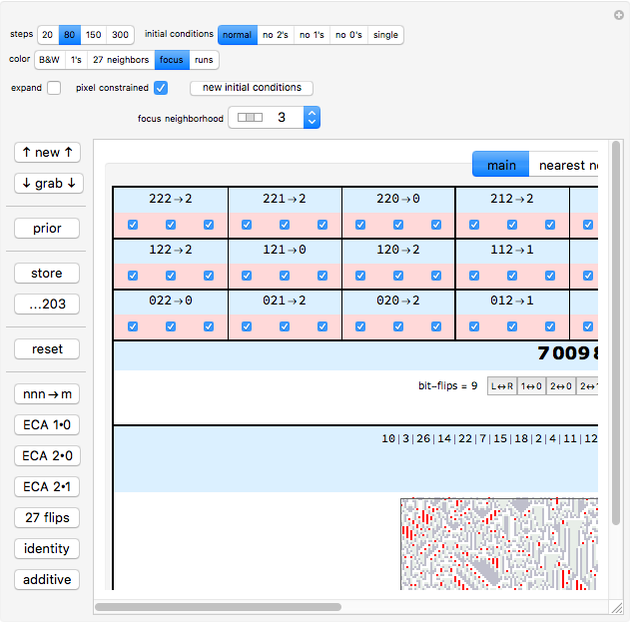
focus: identifies all the locations of one of the 27 neighborhoods chosen in the underlying dropdown menu. Furthermore, a census of the 27 neighborhoods as they appear throughout the entire CA is taken and displayed above the CA. The most common neighborhood is shown to the left, the rarest to the right.
runs: encodes the length of vertical runs of digits. Long runs are shown lighter than short runs. No distinction is made between the three digits 2, 1, 0.
Presets
The "prior" preset button redisplays the prior rule. However, the checkboxes may restore to their default, initial setting. Clicking "↓ grab ↓" works around this.
"store" places the current rule into a memory register. The last three digits of the stored rule are displayed as the label of the next button, which will recall that rule when clicked.
"reset" checks all the checkboxes.
Other presets are available below the "reset" button. Go into the code and modify them to suit your needs. Some presets define subspaces, while others define a specific rule. The "nnn→ m" preset augments any existing setup by adjusting the checkboxes associated with the three neighborhoods (222), (111), and (000), which are unique in that they are composed of just a single digit. Of course, the provided bookmark feature is also available for archiving rules and preset conditions.
"ECA 1•0", "ECA 2•0", and "ECA 2•1" each create a 256-rule subspace that explores all the permutations created by surrounding the 256 elementary cellular automaton (ECA) by the current state of the 19 neighborhoods that are not part of the ECA definition.
"27 flips" forces all the rule bits to flip. It's uncanny how many of these rules are uninteresting, class 2 rules!
"identity" is the opposite of "27 flips". It forces all the rule bits to not flip—the zero flip rule.
"additive" creates a rule in which every pixel transitions to the mod 3 sum of the three digits of the parent neighborhood.
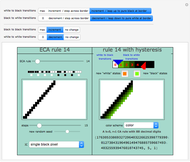
"nearest neighbors" tab
The "nearest neighbors" tab displays the 54 rules that differ from the current rule by just one bit in their base-3 rule specification.
The thumbnails are buttons, so clicking a thumbnail makes that rule the new, current rule.
Thumbnails with green backgrounds identify rules that have one less flip as compared to the current rule. A flip is any neighborhood that is not static from generation to generation.
The thumbnail labels identify the altered rule bit, the new value of the changed bit, and the new rule number. The thumbnails are arranged in nine columns to correspond to the arrangement of the neighborhoods in the main tab.
The "expand" checkbox in the main tab also expands this tab, conveniently eliminating the vertical scrollbars. You can customize the amount of expansion for either the main tab or this tab by modifying the expandedHEIGHT parameter in the program.
"entire subspace" tab
If the current rule subspace contains less than 256 rules, you can view thumbnail versions of all the rules using the "entire subspace" tab. The limit of 256 can be increased by initializing the maxSUBSPACESIZE parameter to a larger value. There is a tradeoff between this threshold value and the overall responsiveness of the Demonstration, so in fact you may want to decrease this value.
A simple subspace is always available by clicking the "↓ grab ↓" button, followed by the "nnn→ m" preset in the main tab. This creates a 27-rule subspace.
The thumbnails are buttons just like the "nearest neighbor" thumbnails, so clicking a thumbnail makes that rule the current rule.
The current rule has a dark-purple background. Rules with light-purple backgrounds have the same number of flips as the current rule, while rules with green backgrounds have one, two, or three fewer flips. All the other rules have more flips.
The left-most thumbnail in the top row corresponds to the rule generated by taking the value of the left-most checked checkbox in all the neighborhood specifications of the main tab. The right-most thumbnail in the bottom row is the rule generated by taking the value of the right-most checked checkbox in all the neighborhood specifications.
Snapshots
Snapshots 1 to 4: alternate color schemes
Permanent Citation