An Introduction to Invariant Subspaces Using a Cube
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
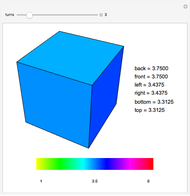
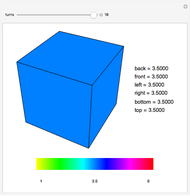
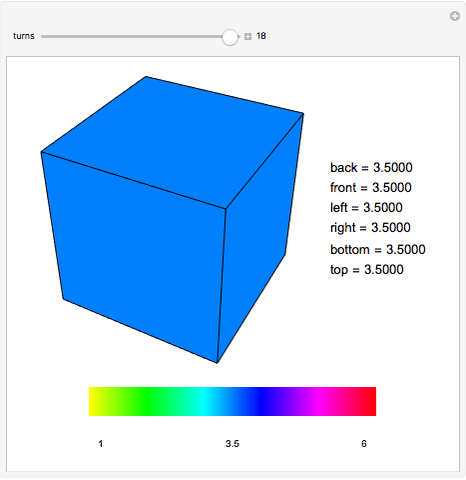
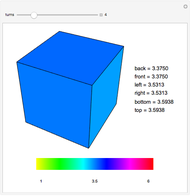
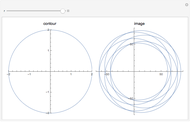
The numbers 1 through 6 are placed on the faces of a cube. At every turn the number on each face is replaced by the average of its four adjacent faces. The value of each face is displayed as a color. The values converge quickly to the average of the initial values of all faces. Think of the collection of values as a six-dimensional vector being acted on at each turn by a linear transformation,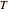 
. The action of the transformation can be completely understood by considering how it acts on each of three 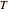-invariant subspaces with direct sum 
.
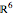Contributed by: Keith Schneider (September 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
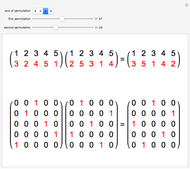
Let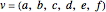 
be a vector in 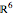, where each component is the value on a face of the cube. It is easy to define the linear transformation 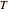that represents a turn. The vector space 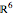can be decomposed into three 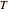-invariant subspaces: 
= {
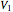| all faces have the same value}, 
={| the sum of all faces is zero and opposite faces have the same value}, and 
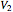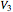={| the sum of all faces is zero and opposite faces also sum to zero}. Examining the action of 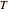on each subspace makes the reasons for the convergence to the average value clear.
Permanent Citation
Combining Two 3D Rotations
George Beck and Jeff Bryant
GL(3,n) Acting on 3D Points
Ed Pegg Jr
Quantum Angular Momentum Matrices
Brad Klee
Spectral Properties of Directed Cayley Graphs
Bill Langhoff
Matrix Representation of the Multiplicative Group of Complex Numbers
Jaime Rangel-Mondragon
Matrix Representation of the Permutation Group
Jaime Rangel-Mondragon
Symmetries of a Square and an Equilateral Triangle
Marc Brodie
Generating 3D Figures with a Given Symmetry Group
Izidor Hafner
Matrix Representation of the Addition Group
S. M. Blinder
Golay Code
Ed Pegg Jr
