Bijective Mapping of an Interval to a Square

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
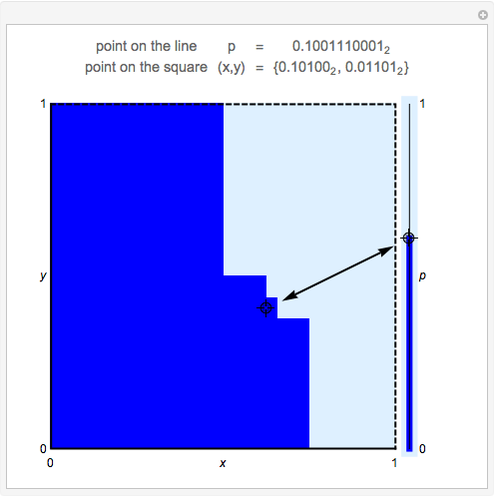
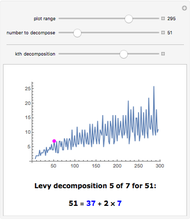
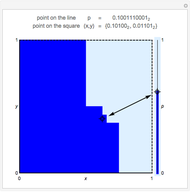
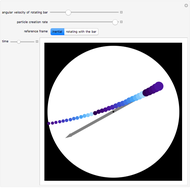
This Demonstration shows a discretized version of a bijective map between points 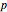 in the unit interval
in the unit interval 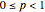 and points
and points 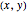 in the unit square, with
in the unit square, with  and
and 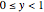 . Each point on the square corresponds to a unique point on the interval and vice versa. This map shows that these one- and two-dimensional sets of points have the same cardinality.
. Each point on the square corresponds to a unique point on the interval and vice versa. This map shows that these one- and two-dimensional sets of points have the same cardinality.
Contributed by: Tad Hogg (April 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
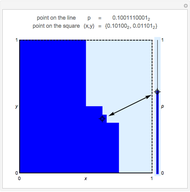
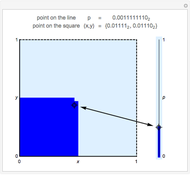
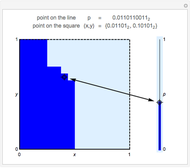
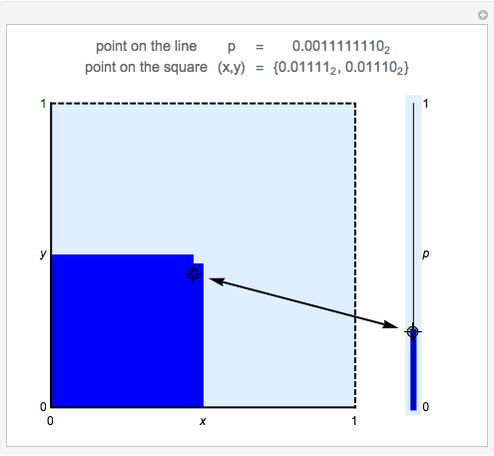
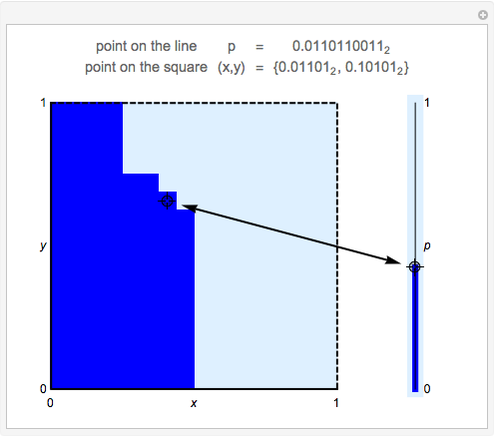
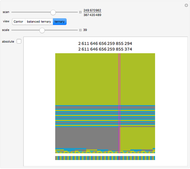
Bijective mappings from the interval to the square are necessarily discontinuous. For example, Snapshots 1 and 2 show the large change in the location of 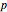 on the line corresponding to a small change in location
on the line corresponding to a small change in location 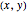 near the center of the square. Similarly, Snapshots 2 and 3 show a small change on the line that corresponds to a large change on the square. The dark blue region of the square corresponds to points mapped to the dark blue region of the interval, that is, points on the interval that are less than or equal to
near the center of the square. Similarly, Snapshots 2 and 3 show a small change on the line that corresponds to a large change on the square. The dark blue region of the square corresponds to points mapped to the dark blue region of the interval, that is, points on the interval that are less than or equal to 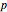 .
.
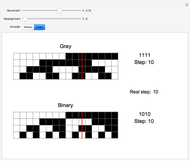
This map uses the binary representation of each number. The map consists of splitting the binary digits of 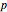 into two groups: the digits in odd locations form the binary digits of
into two groups: the digits in odd locations form the binary digits of  and the even locations form the binary digits of
and the even locations form the binary digits of 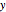 . The discrete version of the mapping uses 10 binary digits of
. The discrete version of the mapping uses 10 binary digits of 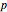 , and hence five binary digits for each of
, and hence five binary digits for each of  and
and 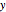 .
.
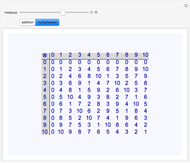
For example, the point 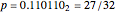 maps to
maps to 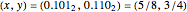 , and vice versa.
, and vice versa.
Permanent Citation