Diffusion to a Spherical Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
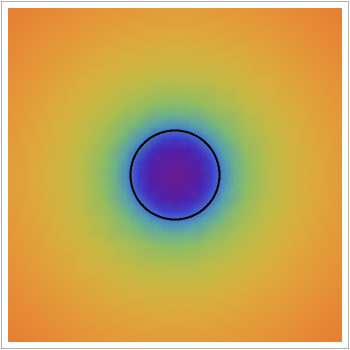
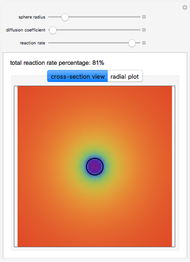
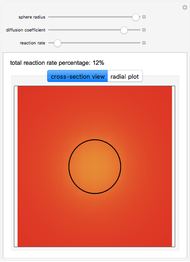
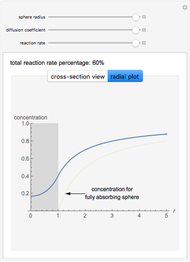
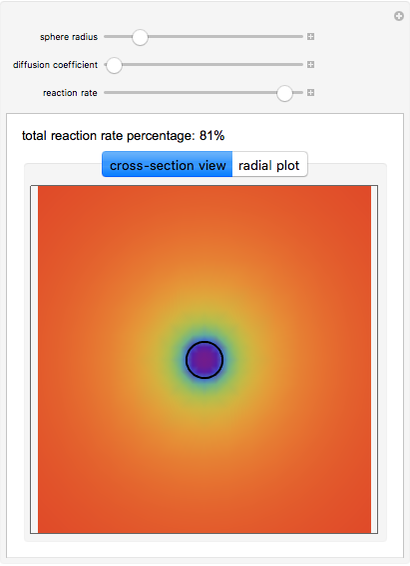
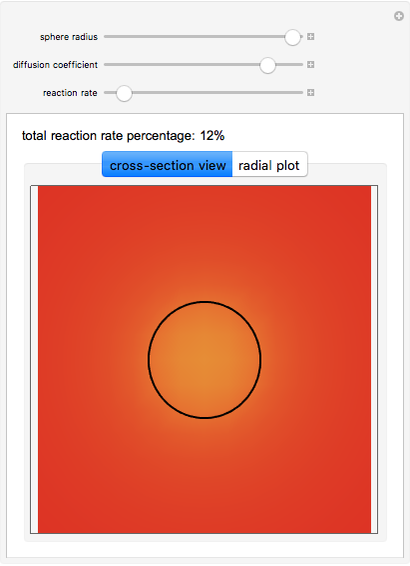
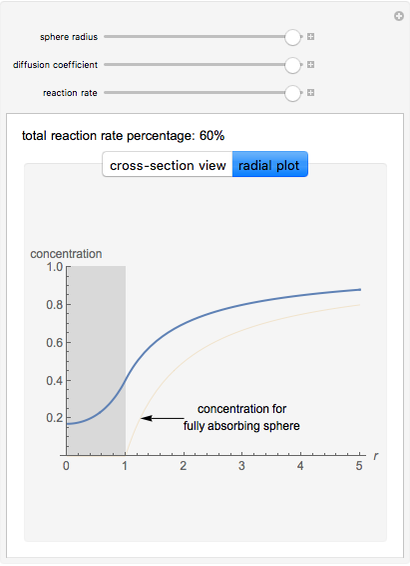
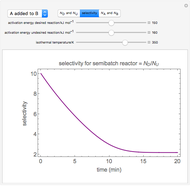
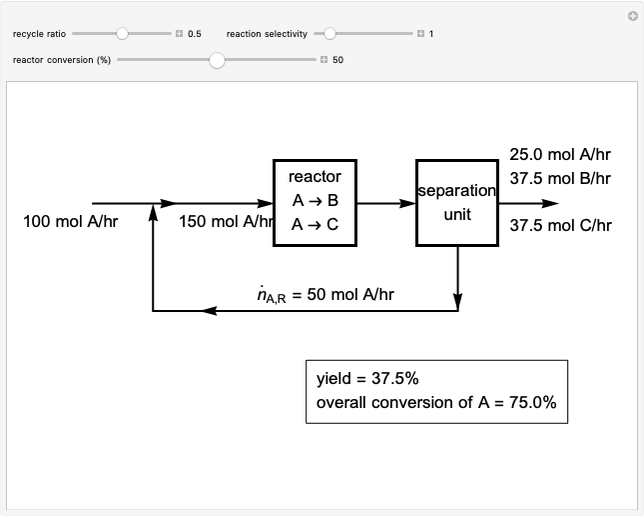
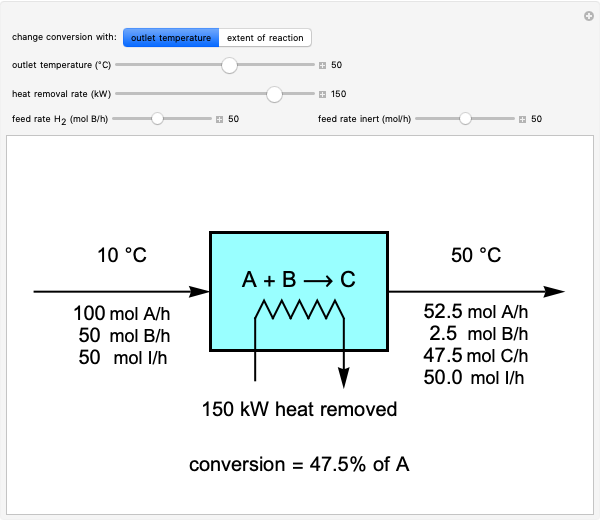
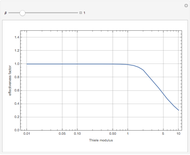
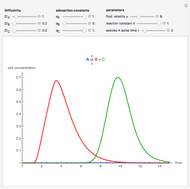
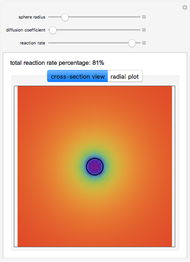
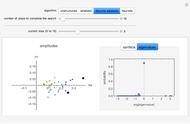
This Demonstration shows the steady-state chemical concentration around and within a spherical chemical reactor that consumes the chemical reaching the sphere via diffusion. The "cross-section view" shows the concentration on a plane through the center of the sphere, with the sphere's surface indicated by the black circle. The "radial view" compares the concentration with that of a fully absorbing sphere of the same size, with the gray region indicating the sphere's interior. The total reaction rate percentage is the rate at which the reactor consumes the chemical relative to the rate for a fully absorbing sphere.
Contributed by: Tad Hogg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The concentration 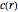 at distance
at distance  from the center of the spherical reactor satisfies the diffusion equation
from the center of the spherical reactor satisfies the diffusion equation 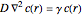 if
if 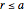 and 0 if
and 0 if 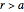 , in spherical coordinates, where
, in spherical coordinates, where  is the diffusion coefficient,
is the diffusion coefficient,  is the radius of the spherical reactor, and
is the radius of the spherical reactor, and  is the reaction rate coefficient. The sphere is in an unbounded fluid. In the units used here, the concentration approaches
is the reaction rate coefficient. The sphere is in an unbounded fluid. In the units used here, the concentration approaches  far from the sphere.
far from the sphere.
The reaction inside the sphere is first-order kinetics, meaning the reaction rate is proportional to the concentration: the number of molecules removed from the fluid per unit time and per unit volume is 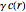 at a position with distance
at a position with distance 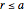 from the center of the sphere. The removal of the chemical in the reactor creates a concentration gradient and hence a diffusion of the chemical from the surrounding fluid into the sphere.
from the center of the sphere. The removal of the chemical in the reactor creates a concentration gradient and hence a diffusion of the chemical from the surrounding fluid into the sphere.
For comparison, the fully absorbing sphere satisfies 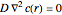 for
for 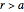 with boundary condition
with boundary condition 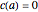 .
.
The fully absorbing sphere gives the maximum possible rate a sphere can absorb the diffusing chemical. The reactor gets close to this maximum by consuming arriving molecules before they have a chance to diffuse back out of the reactor. Achieving this requires the typical distance a molecule in the reactor diffuses before being consumed, 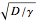 , to be small compared to the radius of the sphere,
, to be small compared to the radius of the sphere,  . In this case, most of the consumption occurs close to the surface of the sphere.
. In this case, most of the consumption occurs close to the surface of the sphere.
H. C. Berg, Random Walks in Biology,  ed., Princeton: Princeton University Press, 1993.
ed., Princeton: Princeton University Press, 1993.
Permanent Citation