Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

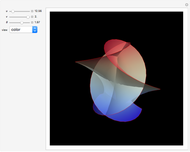
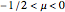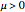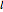Bryant Surfaces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

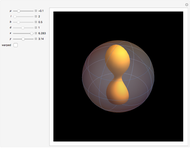
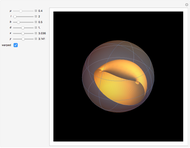
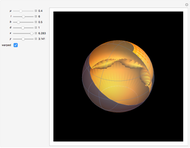
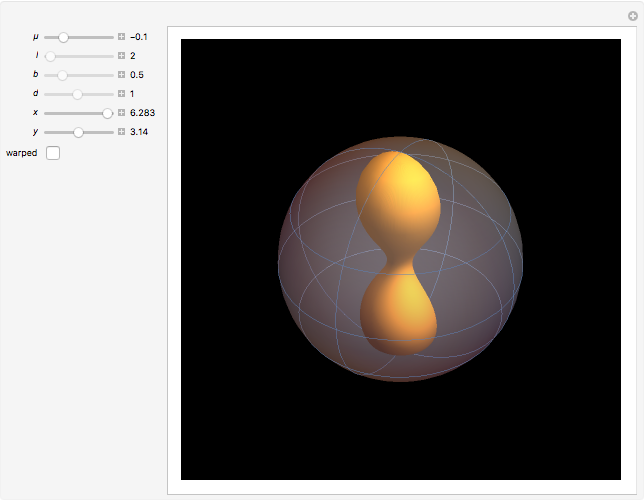
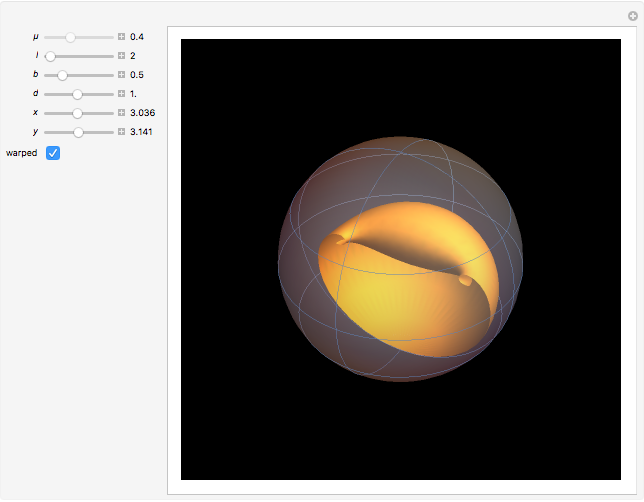
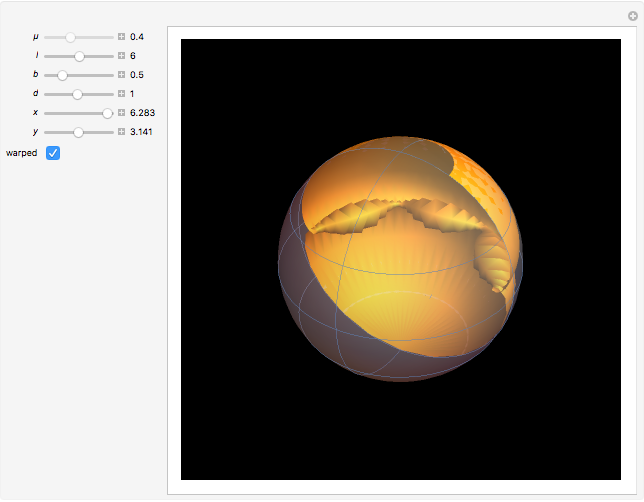
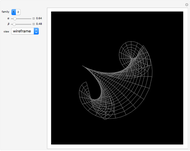
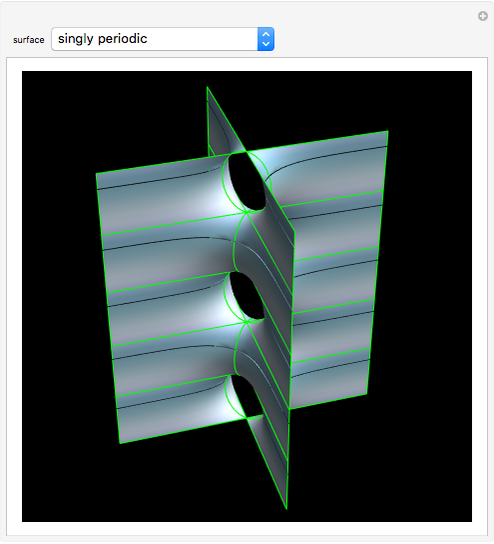
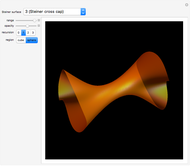
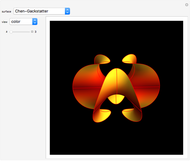
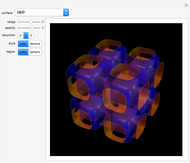
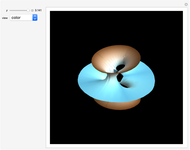
A Bryant surface (or catenoid cousin) is a two-dimensional surface embedded in three-dimensional hyperbolic space with constant mean curvature equal to 1. Bryant derived a holomorphic parameterization for such surfaces, similar to the Weierstrass–Enneper parameterization for minimal surfaces [1, 2].

[more]

A one-parameter family of these surfaces of revolution is defined for the parameter ; for the surface is embedded, and for the surface is not embedded; as tends to zero, the surfaces converge to two horospheres [3, 4, 5]. Another family that arises consists of warped surfaces that are not surfaces of revolution with two regular embedded ends, with warps and parameters and [6, 7]. The parameters and control the range over which the surface is plotted.

[less]

Contributed by: Enrique Zeleny (August 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] Wikipedia. "Hyperbolic Space." (Jul 29, 2014) en.wikipedia.org/wiki/Hyperbolic_space.

[2] R. Bryant, "Surfaces of Mean Curvature One in Hyperbolic Space," Asterisque, 154–155, 1987 pp. 321–347.

[3] W. Rossman, M. Umehara, and K. Yamada. "Mean Curvature 1 Warped Catenoid Cousins in Hyperbolic 3-Space." (Feb 20, 2002) www.eg-models.de/models/Surfaces/Mean_Curvature_Surfaces/2001.01.048/_direct_link.html.

[4] "Binoids: Constant Mean Curvature 1 Surfaces in Hyperbolic 3-Space." GeometrieWerkstatt. (Jul 29, 2014) www.math.uni-tuebingen.de/user/nick/gallery/CMC1Binoid.html.

[5] Wikipedia. "Horosphere." (Jul 29, 2014) en.wikipedia.org/wiki/Horosphere.

[6] W. Rossman, M. Umehara, and K. Yamada. "Mean Curvature 1 Warped Catenoid Cousins in Hyperbolic 3-Space." (Feb 20, 2002) www.eg-models.de/models/Surfaces/Mean_Curvature_Surfaces/2001.01.050/_direct_link.html.

[7] C. Bohle and G. P. Peters, "Bryant Surfaces with Smooth Ends," Communications in Analysis and Geometry, 17(4), 2009 pp. 587–619.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send