Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

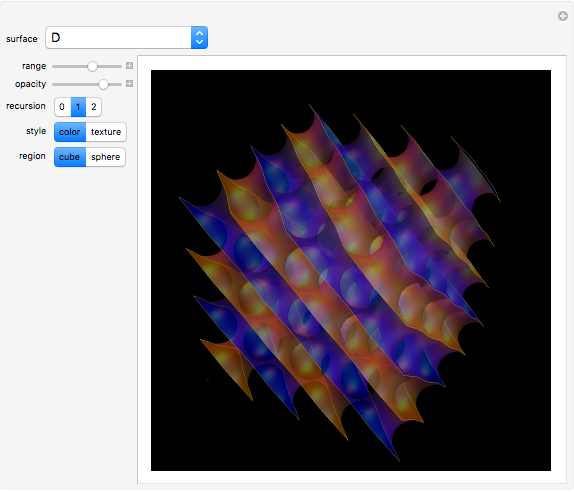
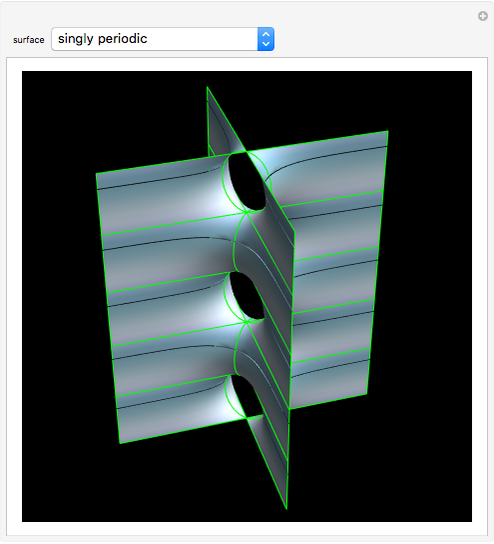
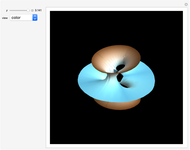
Triply Periodic Minimal Surfaces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

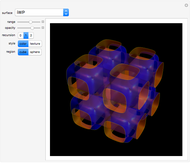
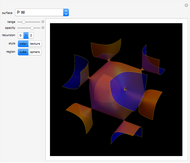
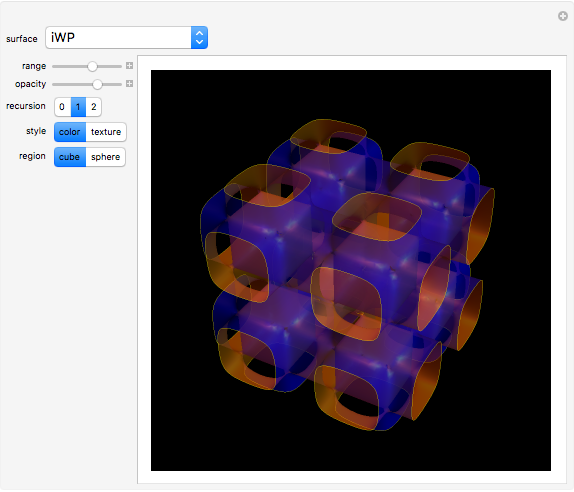
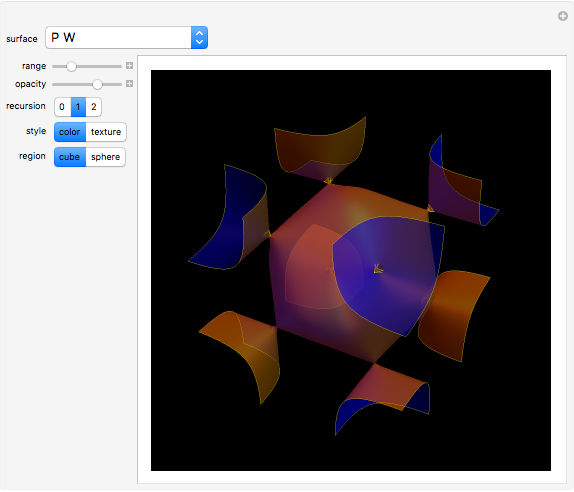
In 1865, H. A. Schwarz found two triply periodic minimal surfaces (P and D) [1] and his student Edwin Neovius found another one (N). Around 1970, Alan Schoen found the gyroid [2] and others; many other cases have been discovered [3, 4]. Such surfaces are relevant in biomaterials and the study of several compounds with cubic lattices [5, 6].

[more]

[5] Fiona Meldrum's Group. "Mechanical Properties of Bio-Inspired Materials." (Aug 7, 2013) http://www.inchm.bris.ac.uk/people/meldrum/mech%20props.html.

[6] P. J. F. Gandy and J. Klinowski, "The Equipotential Surfaces of Cubic Lattices,", Chemical Physics Letters, 360(5–6), 2002 pp. 543–551. doi:10.1016/S0009-2614(02)00864-3.

[less]

Contributed by: Enrique Zeleny (August 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] A. H. Schoen, Infinite Periodic Minimal Surfaces without Self-Intersections, NASA Technical Note TN D-5541, Washington, DC: National Aeronautics and Space Administration, 1970.

[2] E. Zeleny. "The Gyroid" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/TheGyroid.

[3] The Scientific Graphics Project. "Minimal Surfaces." (Aug 7, 2013) archive.msri.org/about/sgp/jim/geom/minimal/index.html.

[4] K. Brakke. "Triply Periodic Minimal Surfaces." (Aug 7, 2013) www.susqu.edu/facstaff/b/brakke/evolver/examples/periodic/periodic.html.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send