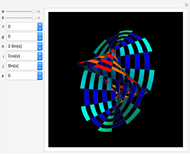
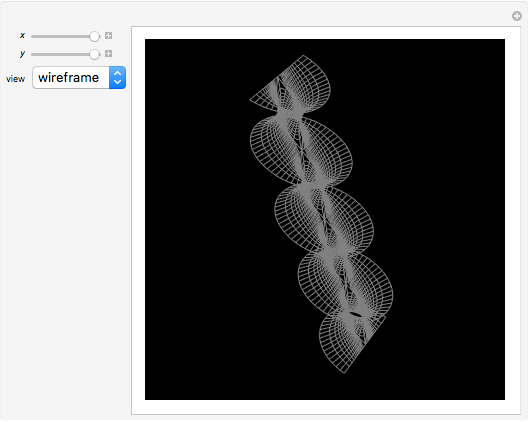
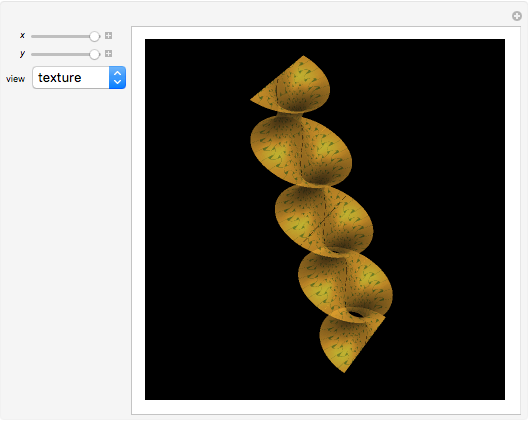
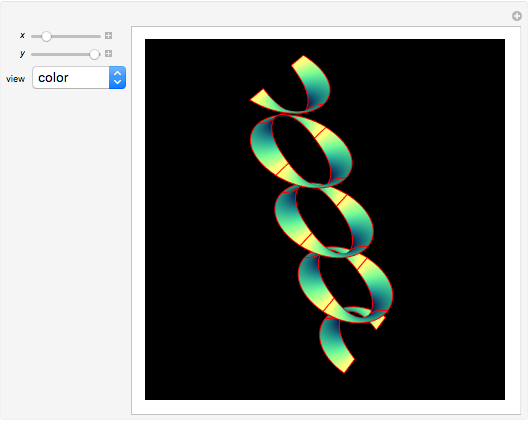
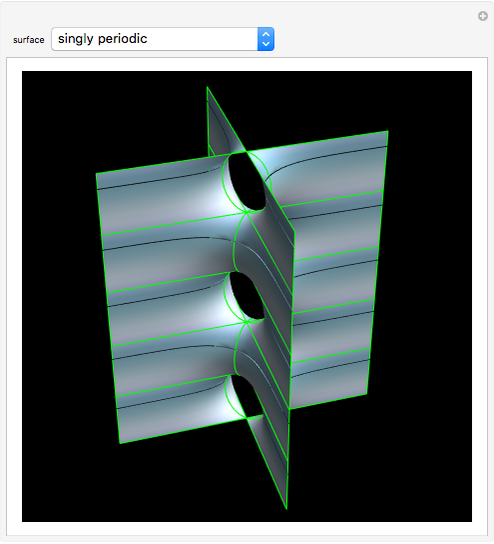
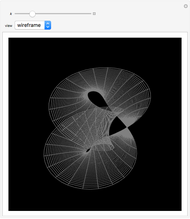
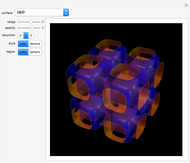
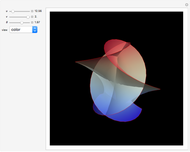
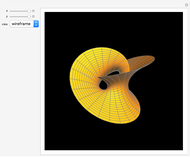
Riemann's minimal surface is a family of singly periodic embedded minimal surfaces discovered by Bernhard Riemann and published after his death in 1866. The surfaces have an infinite number of ends in parallel planes, foliated by horizontal circles, converging to helicoids or catenoids. The parametrization presented here is based on [1], using the Weierstrass representation, given in terms of elliptic functions.