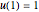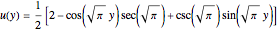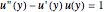Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Chebyshev Collocation Method for Linear and Nonlinear Boundary Value Problems

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

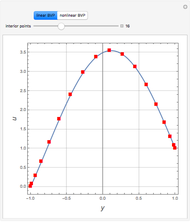
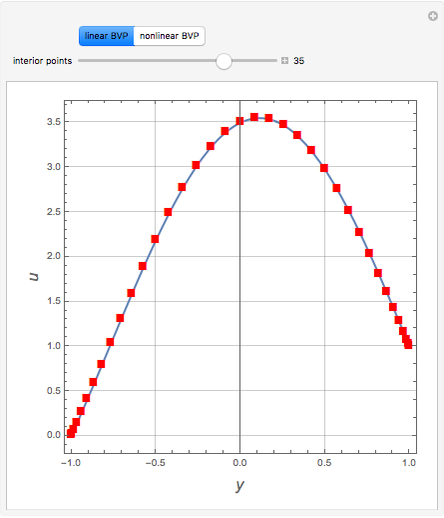
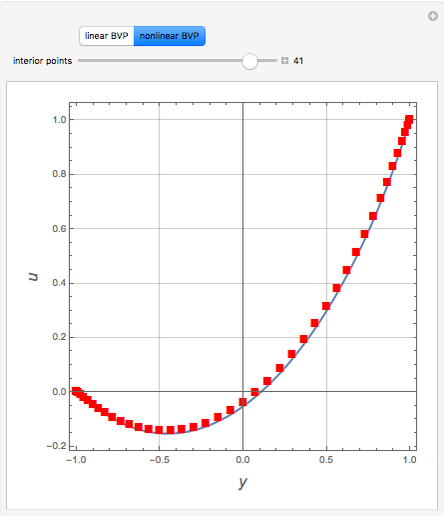
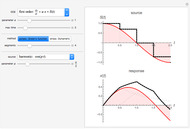
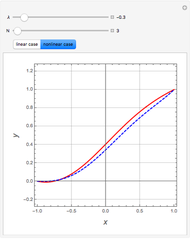
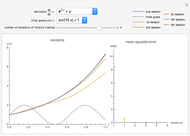
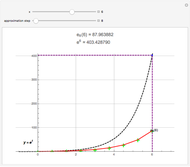
Consider two boundary-value problems (BVP), one linear and the other nonlinear.

[more]

The linear problem is defined by , with the boundary conditions and . This problem admits an analytical solution given by , displayed in blue when you click the linear BVP tab.

The nonlinear problem statement is , where again, and . This problem is solved numerically and the solution is shown in blue when you click the nonlinear BVP tab.

This Demonstration compares these two solutions to those obtained using the Chebyshev collocation method. You can set the number of interior points, , and the results of the Chebyshev collocation technique are plotted as red solid squares. The agreement between the two solutions is very good if you choose a relatively large number of interior points (e.g., ).

[less]

Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (February 2013)
Open content licensed under CC BY-NC-SA

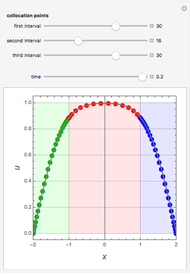
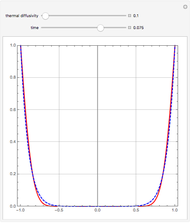
Snapshots

Details

The linear BVP requires solving a system of linear equations, which is readily done using LinearSolve.

The nonlinear BVP involves a system of nonlinear algebraic equations, which can be conveniently solved using FindRoot.

In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by .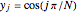

The 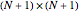Chebyshev derivative matrix at quadrature points, 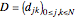, is given by:

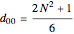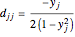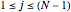, , for and for and ,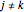

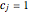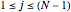where for and .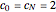

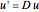The matrix is used this way: and .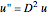

References

[1] P. Moin, Fundamentals of Engineering Numerical Analysis, Cambridge, UK: Cambridge University Press, 2001.

[2] S. Biringen and C.-Y. Chow, An Introduction to Computational Fluid Mechanics by Example, Hoboken, NJ: John Wiley & Sons, 2011.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send