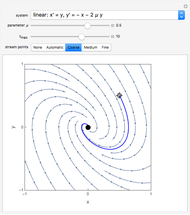
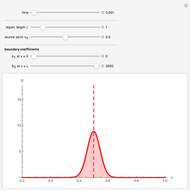
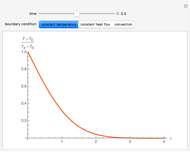
Solution to Differential Equations Using Discrete Green's Function and Duhamel's Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
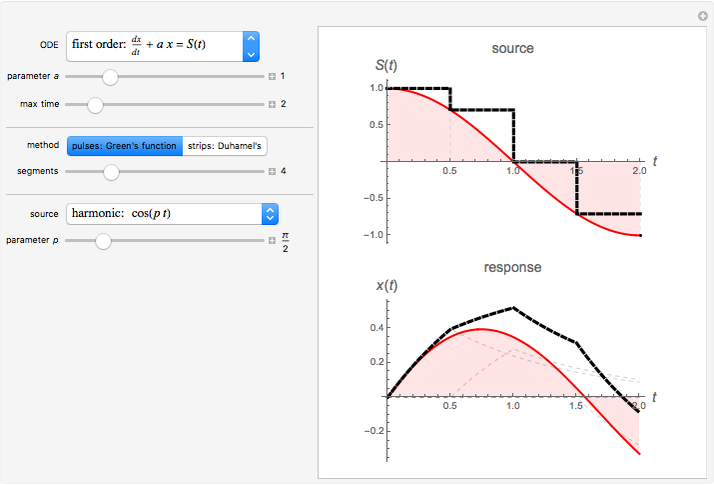
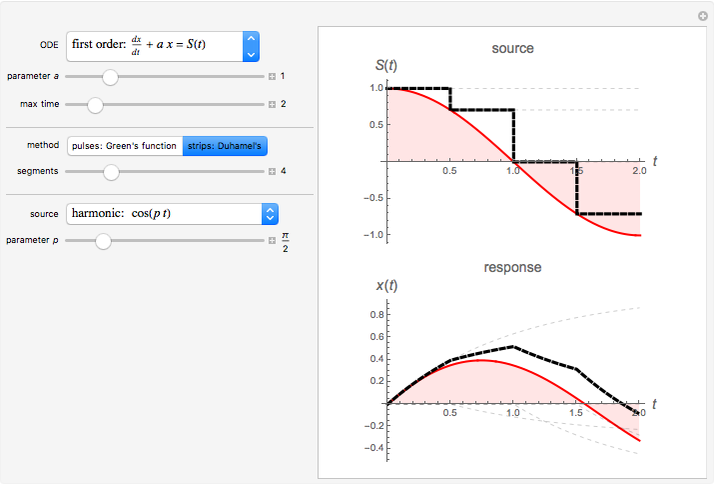
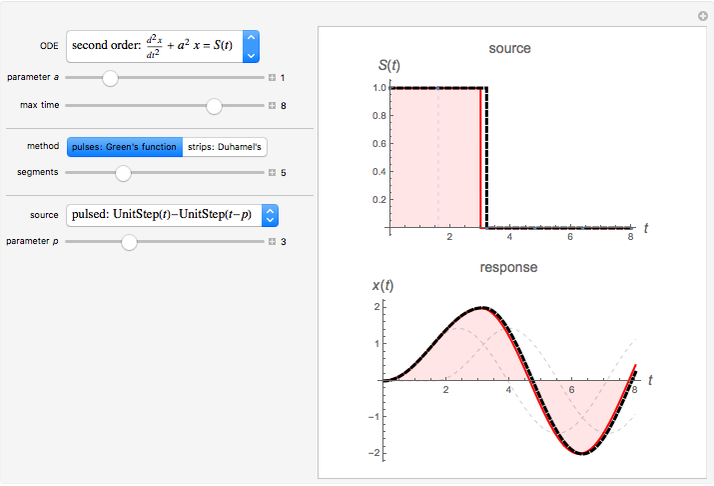
This Demonstration shows how to find approximate solutions to linear ordinary differential equations using two methods:
[more]
Contributed by: Jason Beaulieu and Brian Vick (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
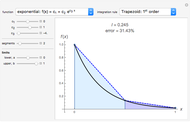
Linear problems can be constructed by using a linear combination from simpler subproblems. If the forcing function is expressed as 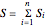 , then the total solution can be expressed as
, then the total solution can be expressed as  , where
, where 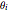 is the response to
is the response to 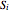 . In this Demonstration, we have decomposed the forcing function,
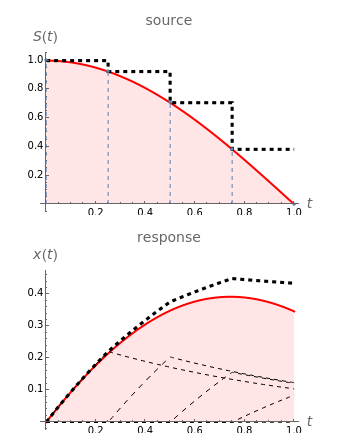
. In this Demonstration, we have decomposed the forcing function, 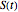 , as a sequence of either pulses or strips. This method can be extended to solve problems that contain other types of forcing functions such as volumetric sources, surface sources, and initial conditions. The approximate solution with multiple forcing functions can be found by superimposing each response to the individual forcing functions.
, as a sequence of either pulses or strips. This method can be extended to solve problems that contain other types of forcing functions such as volumetric sources, surface sources, and initial conditions. The approximate solution with multiple forcing functions can be found by superimposing each response to the individual forcing functions.
The pulse method uses the linearity property to construct the total response by the addition or superposition of the responses to all the pulses. This method is a discrete version of the Green's function technique. In the limit as 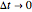 , the method reduces to the usual Green's function method. Similarly, the strip method finds the total response by the superpostion of responses to all the strips. This method is particularly useful in the time variable rather than the spatial variable, because time runs indefinitely, while space is typically limited to a finite region. This method is a discrete analog of Duhamel's method. By taking the limit as
, the method reduces to the usual Green's function method. Similarly, the strip method finds the total response by the superpostion of responses to all the strips. This method is particularly useful in the time variable rather than the spatial variable, because time runs indefinitely, while space is typically limited to a finite region. This method is a discrete analog of Duhamel's method. By taking the limit as 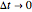 , Duhamel's method is obtained. Each method has its advantages and disadvantages, but they result in the same level of approximation.
, Duhamel's method is obtained. Each method has its advantages and disadvantages, but they result in the same level of approximation.
Permanent Citation