Solution of the Laplace Equation Using Coordinates Fitted to the Boundary Conditions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
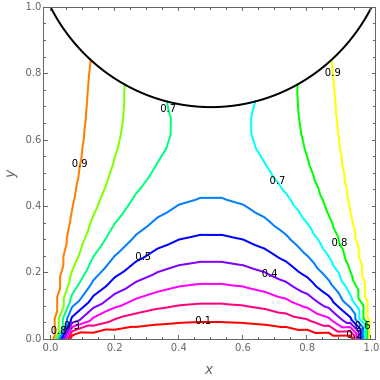
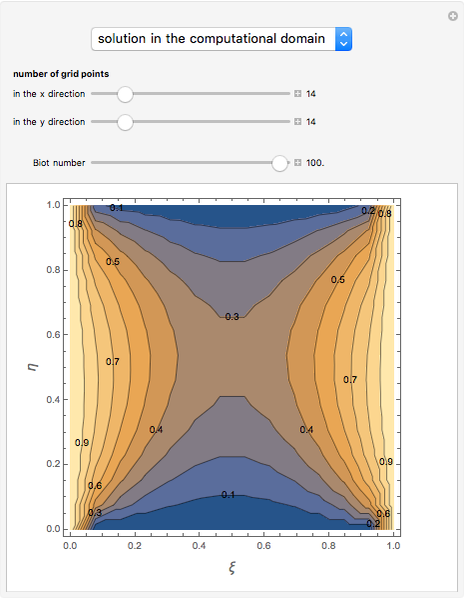
This Demonstration solves the 2D steady-state heat conduction equation in a physical domain that does not conform to an orthogonal coordinate system. The physical domain is mapped onto a unit square using boundary-fitted coordinates. The transformed heat conduction equation in the computational domain is then solved using a central-difference finite-difference scheme. You can vary the number of grid points in the  and
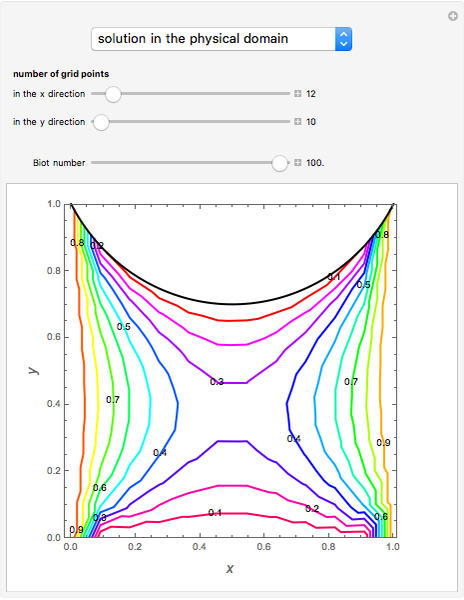
and  directions of the computational domain as well as the Biot number parameter for heat transfer from the upper surface. The resulting isotherms are shown for both the physical and computational domains. The mapping of the grid points from the
directions of the computational domain as well as the Biot number parameter for heat transfer from the upper surface. The resulting isotherms are shown for both the physical and computational domains. The mapping of the grid points from the  -
- computational domain to the
computational domain to the  -
- points in the physical domain is also shown.
points in the physical domain is also shown.
Contributed by: Brian G. Higgins and Housam Binous (October 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Background
Undergraduate students are often exposed to various numerical methods for solving partial differential equations. For example, in a sophomore engineering heat-transfer course, the finite-difference method is introduced to solve steady-state heat conduction problems, in which the computational domain conforms to one of the traditional orthogonal coordinate systems (i.e., rectangular, cylindrical, or spherical). In this Demonstration, we consider a 2D steady-state heat conduction problem in a physical domain based on a nonstandard orthogonal coordinate system:
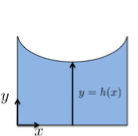
We show how this problem can be solved using a traditional central-difference method with boundary-fitted coordinates.
The steady-state temperature distribution in the cavity is described by the following boundary-value problem (BVP) with four boundary conditions (BC1–BC4):
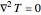 ,
,
BC1:  for
for  and
and  ,
,
BC2: 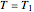 for
for  and
and  ,
,
BC3: 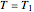 for
for 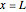 and
and 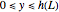 ,
,
BC4: 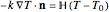 for
for 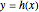 and
and  .
.
The upper boundary 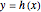 is specified as an arc of a circle, given by
is specified as an arc of a circle, given by 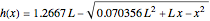 , and has unit normal
, and has unit normal 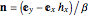 ,
, 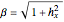 .
.
Dimensionless Variables
It is desirable to make the BVP dimensionless before attempting to solve it numerically. We introduce the following dimensionless variables:
 ,
, 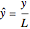 ,
, 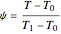 and
and 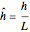 .
.
The dimensionless form of the equations becomes:
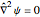 ,
,
BC1:  for
for  and
and 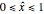 ,
,
BC2:  for
for 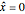 and
and 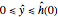 ,
,
BC3:  for
for  and
and 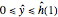 ,
,
BC4: 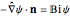 for
for 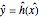 and
and 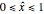 ,
,
where 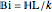 is the Biot number.
is the Biot number.
The interface equation becomes:
 .
.
For notational convenience, we suppress the hat ( ) notation and use the above formulation in what follows.
) notation and use the above formulation in what follows.
Boundary-Fitted Coordinates
The physical domain is defined by the coordinates  and
and  .
.
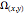 :
: 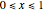 ,
,  .
.
We now suppose that we have the following mapping that maps the physical domain 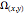 into a unit square in the computational domain:
into a unit square in the computational domain:
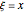 ,
, 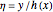 ,
,
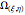 :
: 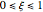 ,
,  .
.
Thus the dimensionless temperature profile in the computational domain is defined by the mapping: 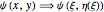 . We can use the chain rule for differentiation to determine the explicit form for the Laplacian
. We can use the chain rule for differentiation to determine the explicit form for the Laplacian 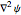 in the transformed coordinates (ξ, η).
in the transformed coordinates (ξ, η).
Thus
 .
.
Clearly when  s uniform (flat) then
s uniform (flat) then  and we get:
and we get:
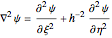 ,
which is the Laplacian in rectangular coordinates with
,
which is the Laplacian in rectangular coordinates with  scaled with the height
scaled with the height  .
.
Finite Difference Solution
To generate our finite-difference formula, we use the following grid template:
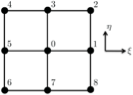
and use central differences for all derivatives. Thus at node  , we have the following approximation for the function
, we have the following approximation for the function  :
:
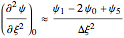 ,
,
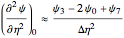 ,
,
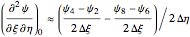 ,
,
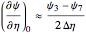 .
.
Thus the discretized version of the Laplacian of ψ at an interior node 0 is given by
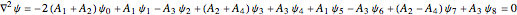 ,
,
where the coefficients 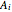 are given by
are given by
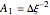 ,
, 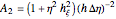 ,
,
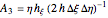 ,
, 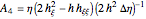 .
.
Once the grid is specified, then the coefficients 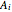 can be computed at the given node, for a given
can be computed at the given node, for a given 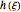 .
.
Boundary Conditions at the Interface
At the interface, the heat flux is given by
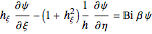 at
at  .
.
We will use a central-difference scheme for this BC:
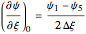 and
and 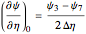 ,
,
which introduces a fictitious node 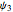 that lies outside the domain:
that lies outside the domain:
 ,
,
where
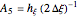 and
and 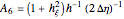 .
.
Solving for the fictitious node, we get
 .
.
References
[1] C. Chen and J. M. Floryan, "Numerical Simulation of Nonisothermal Capillary Interfaces," Journal of Computational Physics, 111(1), 1994 pp. 183–193. doi:10.1006/jcph.1994.1053.
[2] M. Hamed and J. M. Floryan, "Marangoni Convection. Part 1. A Cavity with Differentially Heated Sidewalls," Journal of Fluid Mechanics, 405, 2000 pp. 79–110. journals.cambridge.org/abstract_S002211209900734X.
Permanent Citation