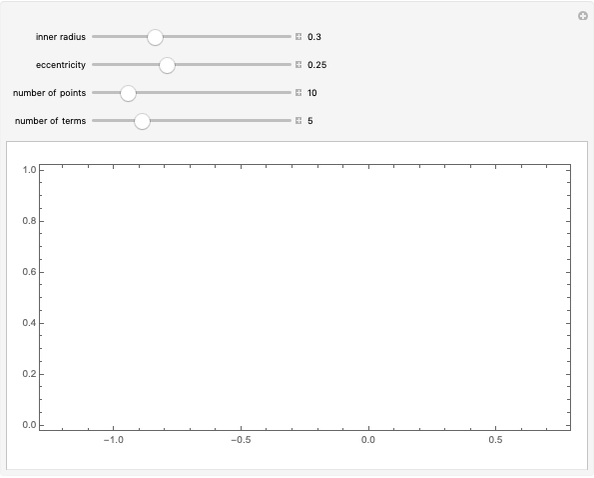
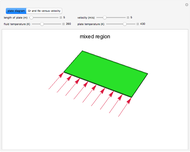
Convection between Two Vertical Walls

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
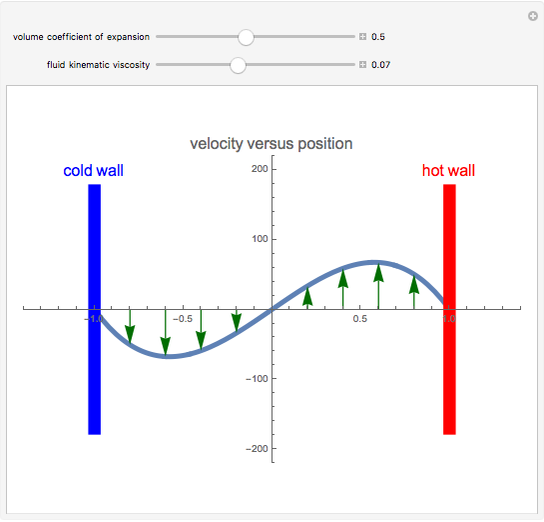
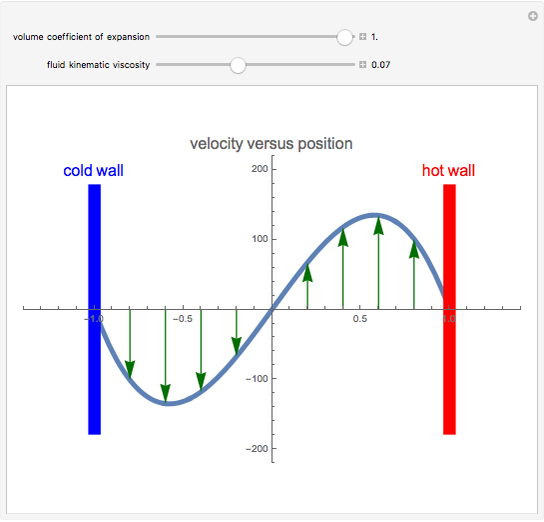
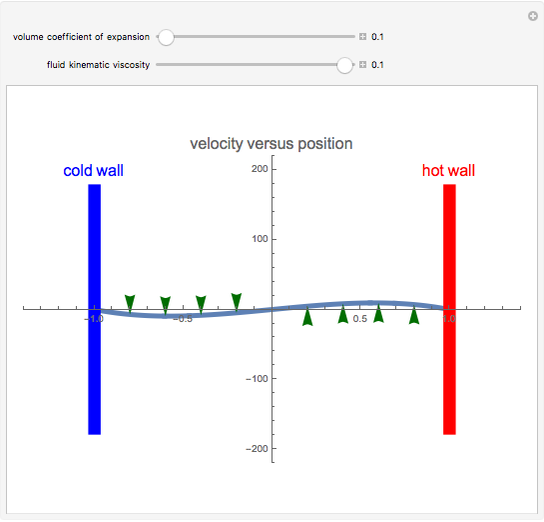
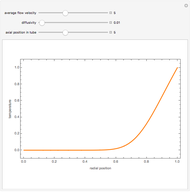
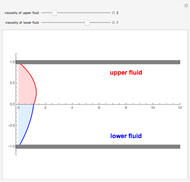
Two parallel walls are maintained at uniform temperatures (a hot temperature, 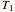 , and a cold temperature,
, and a cold temperature,  ). You can set the viscosity and volume coefficient of expansion of the fluid that fills the space between the two walls. The steady state velocity profile of the resulting natural convection is displayed.
). You can set the viscosity and volume coefficient of expansion of the fluid that fills the space between the two walls. The steady state velocity profile of the resulting natural convection is displayed.
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The temperature variation in the  direction is assumed to be linear:
direction is assumed to be linear:
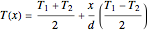 , where
, where 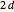 is the space between the two walls.
is the space between the two walls.
The density is not constant and varies according to 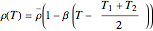 , where
, where  is the density at the mean temperature,
is the density at the mean temperature, 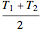 .
.
The governing equation is given by  .
.
It is possible to derive an analytical expression of the dimensionless velocity using the built-in Mathematica function DSolve:
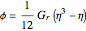 ,
,
where  is the dimensionless velocity,
is the dimensionless velocity,  the dimensionless length, and
the dimensionless length, and 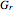 the Grashof number, a dimensionless number that arises in problems on free convection.
the Grashof number, a dimensionless number that arises in problems on free convection.
Permanent Citation