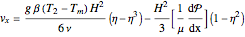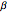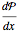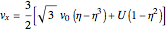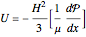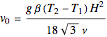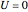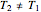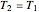Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Flow in a Vertical Channel with Walls at Different Temperatures

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

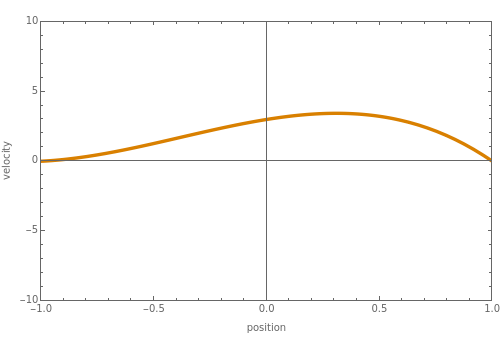
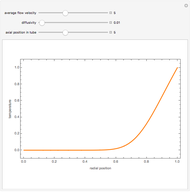
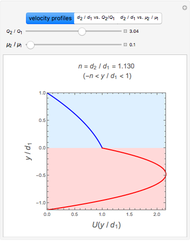
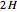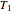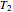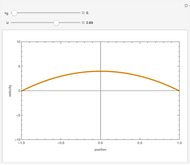
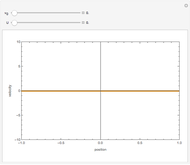
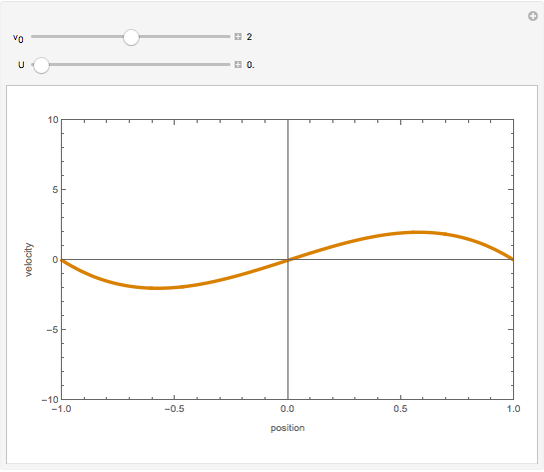
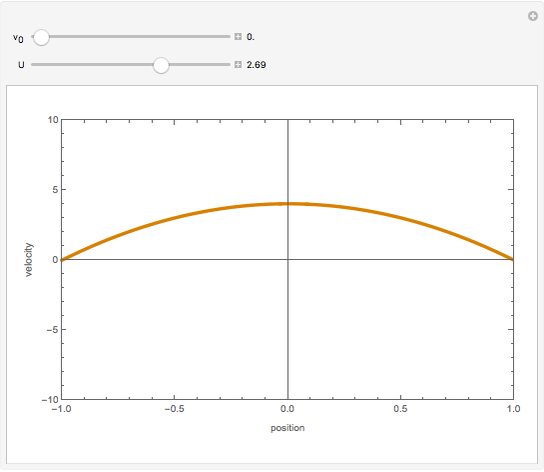
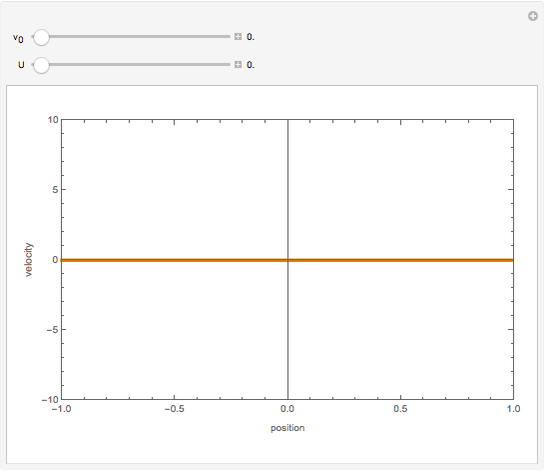
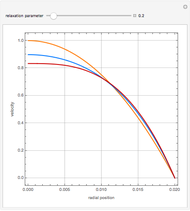
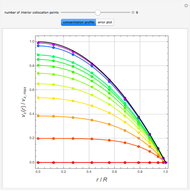
Consider a vertical parallel-plate channel of width with walls at different temperatures and , 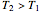. Two cases are studied: (1) pure free convection (i.e., the channel is closed at both ends and there is no net flow); and (2) mixed free and forced convection (a pressure gradient is present). The velocity (solution of the momentum equation) is given by

[more]

,

where is gravitational acceleration, is the thermal expansion coefficient, is the reference temperature taken equal to the mean temperature, is the kinematic viscosity, is the dynamic viscosity, is the pressure gradient, and is the dimensionless position.

The velocity can be expressed as , where is the mean velocity and is the maximum velocity when the pressure gradient is zero.

If and , one recovers pure free convection. When , the velocity profile is the expected parabolic profile corresponding to a Poiseuille flow. In general, mixed free and forced convection is observed.

[less]

Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

W. M. Deen, Analysis of Transport Phenomena, New York: Oxford University Press, 1998.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send