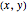Coupler Curve Atlas for the Four-Bar Linkage

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
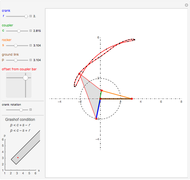
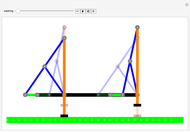
In the design of mechanisms, linkages are used to create motions with a specific course of position and speed.
[more]
Contributed by: Erik Mahieu (May 2016)
Open content licensed under CC BY-NC-SA
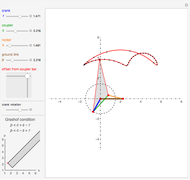
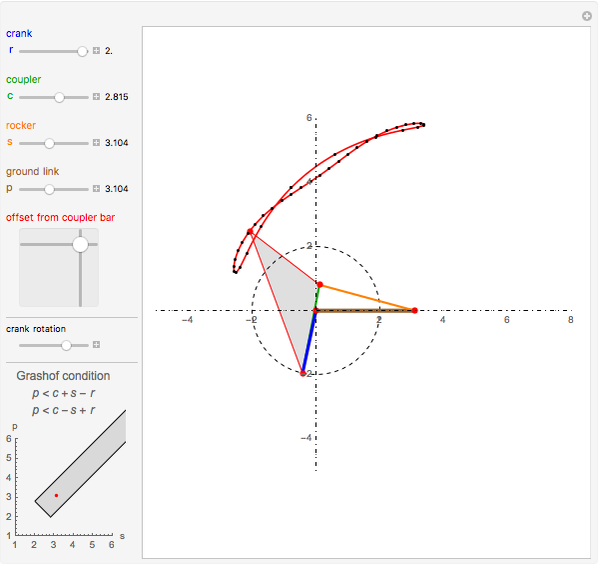
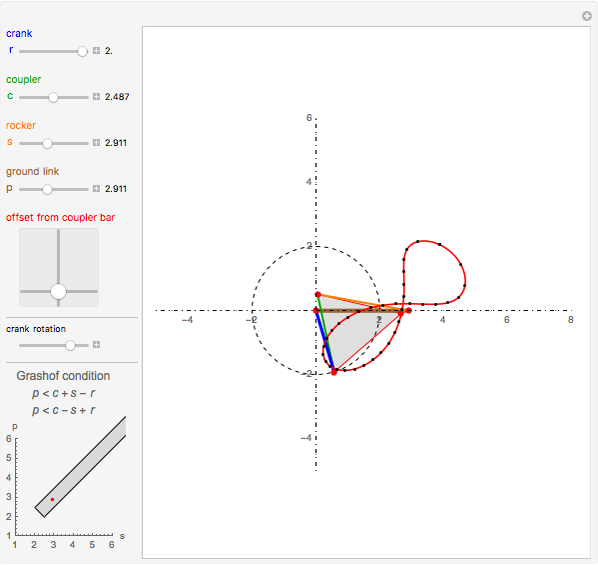
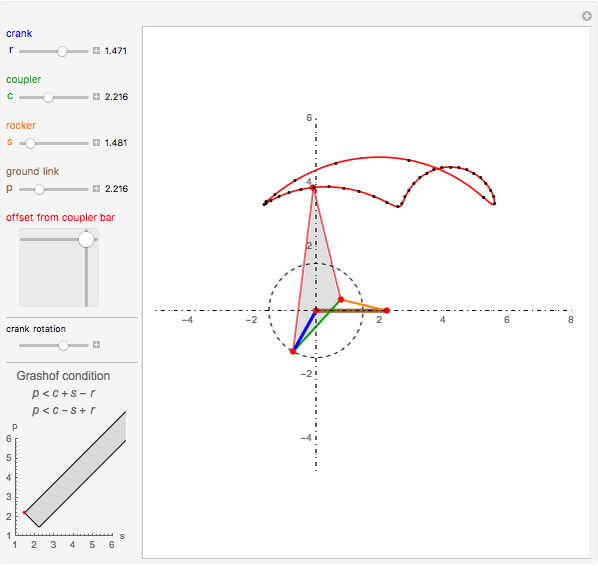
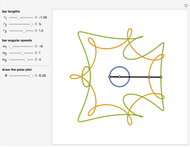
Snapshots
Details
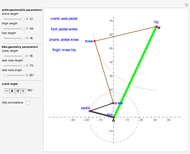
In order to be of the crank-rocker type, the links have to meet Grashof's law [1], which states that the sum of the longest and the shortest link must be less than or equal to the sum of the remaining two links. This condition must be met to allow at least one link to make a complete revolution.
The Freudenstein equation [3] is used to compute the angular positions of the linkage bars.
References
[1] "Grashof's Law." eNotes: Mechanical Engineering. (May 23, 2016) engineeronadisk.com/notes_mechanic/mechanismsa6.html.
[2] J. A. Hrones and G. L. Nelson. Analysis of the Four Bar linkage: Its Application to the Synthesis of Mechanisms, Scribd. www.scribd.com/doc/214820022/Hrones-and-Nelson-Atlas.
[3] A. Ghosal. "The Freudenstein Equation and Design of Four-link Mechanisms." (May 23, 2016) www.mecheng.iisc.ernet.in/~asitava/resonance10.pdf.
Permanent Citation