Wald and Bayesian Confidence Intervals

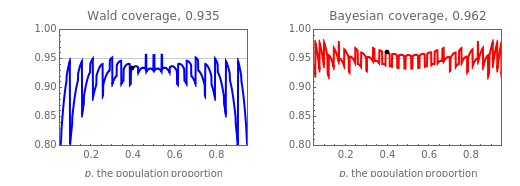
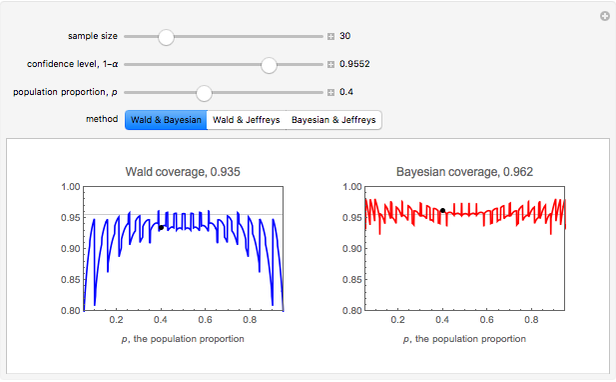
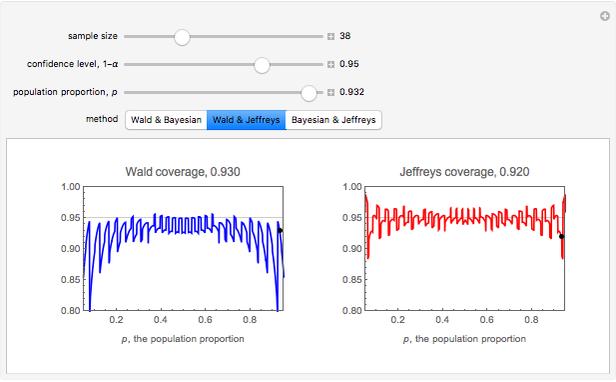
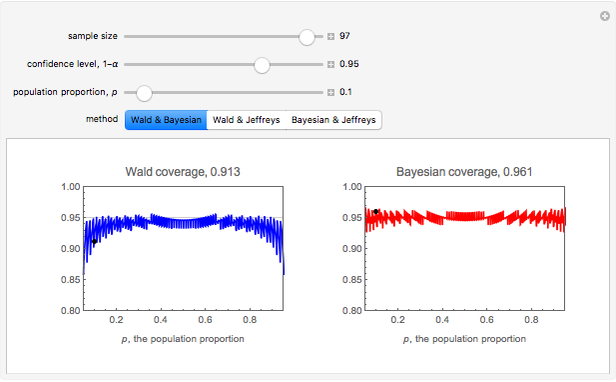
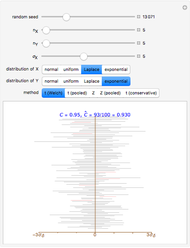
Nearly every introductory textbook on statistics describes a technique for constructing a confidence interval for a population proportion based on the normal distribution approximation to the binomial distribution. This interval is commonly known as the Wald interval and is nearly universally used for obtaining confidence intervals for proportions. The Wald interval is based on the idea that as the sample size gets large, the binomial distribution may be approximated by the Gaussian (normal) distribution. Thus one might suspect that the Wald technique would provide adequate or very reliable confidence intervals (i.e., intervals that provide coverage nearly equal to the desired confidence level), especially as the sample size increases. In fact, this is not the case. It can be shown that the Wald interval displays erratic behavior with respect to coverage, even when sample sizes are quite large. Additionally, the behavior of these intervals is erratic even for values of near 0.5, which might seem counterintuitive.