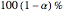One-Sample t-Test and Confidence Interval with Dot Chart in Small Samples

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
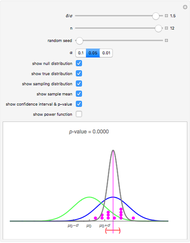
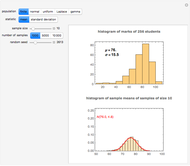
The dot chart represents a random sample of size  from a normal distribution, shown in blue, with mean
from a normal distribution, shown in blue, with mean  and standard deviation
and standard deviation  . This is the true distribution. This Demonstration focuses on the null hypothesis,
. This is the true distribution. This Demonstration focuses on the null hypothesis, 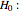
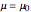 . For hypothesis testing, it is assumed that the sample is from a normal population with unknown mean and unknown variance. The hypothetical distribution,
. For hypothesis testing, it is assumed that the sample is from a normal population with unknown mean and unknown variance. The hypothetical distribution, 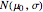 , is shown in green. When
, is shown in green. When 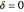 , the null distribution and true distribution are the same, but otherwise they are different.
, the null distribution and true distribution are the same, but otherwise they are different.
Contributed by: Douglas Woolford and Ian McLeod (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
We focus on small samples, 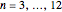 to avoid resizing and thus distorting the graphic, which is an important consideration for dynamic plots.
to avoid resizing and thus distorting the graphic, which is an important consideration for dynamic plots.
Snapshot 1: A new sample with 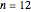 instead of
instead of  . The width of the confidence interval is slightly larger than in the thumbnail as might be expected. But click the "random seed" slider "+" button and then click the play button to see there is considerable variation in the size of the confidence interval. This is because the t-test is used. If a
. The width of the confidence interval is slightly larger than in the thumbnail as might be expected. But click the "random seed" slider "+" button and then click the play button to see there is considerable variation in the size of the confidence interval. This is because the t-test is used. If a  test were used, the width of the confidence interval would only depend on
test were used, the width of the confidence interval would only depend on  and
and  and not on the actual data.
and not on the actual data.
Snapshot 2: Same setting as snapshot 1 but a new sample. Notice the sampling distribution has changed and is not quite so centered over the true distribution. In this case, the confidence interval is actually wider than snapshot 1 and even wider than the case when  . This is due to randomness.
. This is due to randomness.
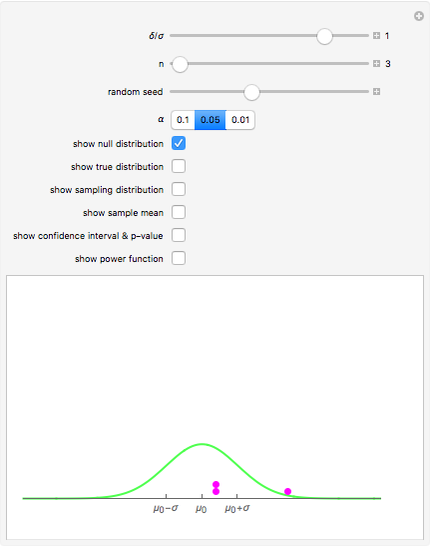
Snapshot 3: This scenario provides a teaching simulation. The instructor might say, "I think the average height of men in this class is about 5.5 feet". The null distribution with 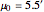 is shown. The dot chart shows the results of a simulated sample of size 3. In this case, all the observations are greater than
is shown. The dot chart shows the results of a simulated sample of size 3. In this case, all the observations are greater than 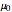 .
.
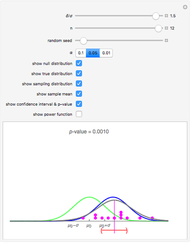
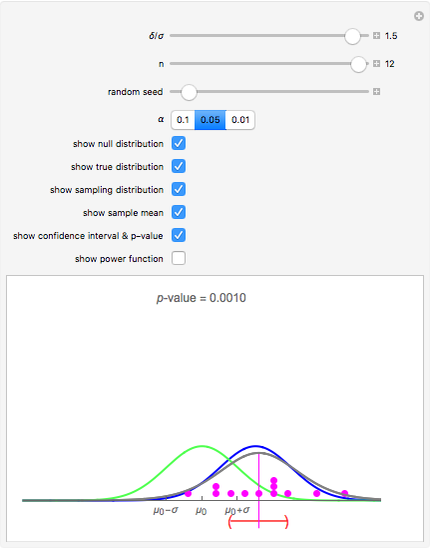
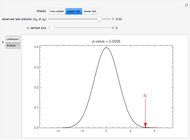
Snapshot 4: The 95% confidence and the 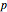 -value are now shown. The 95% confidence interval includes
-value are now shown. The 95% confidence interval includes 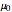 and the
and the 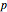 -value is 0.1888 so there is evidence against finding
-value is 0.1888 so there is evidence against finding 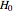 could easily be due to chance. We have used a two-sided test, which is more conservative than one-sided alternatives. In general, as recommended in [1] §1.8, one-sided tests may, in actual practice, too easily result in spurious findings and so are not recommended.
could easily be due to chance. We have used a two-sided test, which is more conservative than one-sided alternatives. In general, as recommended in [1] §1.8, one-sided tests may, in actual practice, too easily result in spurious findings and so are not recommended.
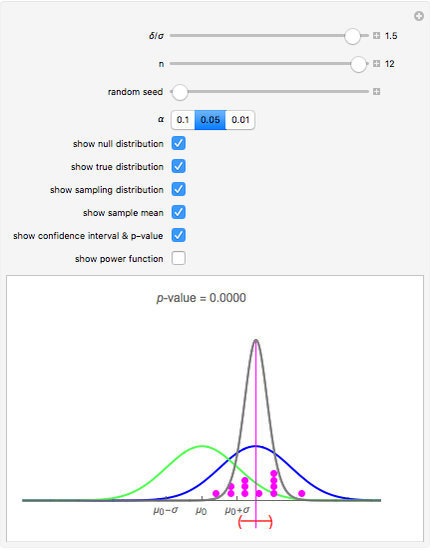
Snapshot 5: Increasing the size of sample to  provides strong evidence that
provides strong evidence that 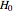 is not true.
is not true.
Snapshot 6: Let 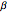 and
and 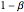 denote the probability of a type II error and power, respectively. The power curve,
denote the probability of a type II error and power, respectively. The power curve, 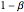 versus
versus 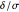 , for the two-sample t-test when
, for the two-sample t-test when  and
and 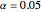 is shown. By symmetry, the curve is only shown for
is shown. By symmetry, the curve is only shown for 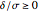 . Green is used to indicate the power at the set value of
. Green is used to indicate the power at the set value of  , in this case
, in this case  . In planned experiments, usually a minimum power of 90% is desired and the green lines indicate the size of
. In planned experiments, usually a minimum power of 90% is desired and the green lines indicate the size of 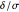 needed to attain 90% power. So from the plot we see that
needed to attain 90% power. So from the plot we see that  ,
, 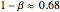 and that to achieve 90% we would need
and that to achieve 90% we would need  . Another way 90% could be achieved is by increasing the sample size
. Another way 90% could be achieved is by increasing the sample size  . Slide
. Slide  up to 12 and you see that we can attain about 90% with
up to 12 and you see that we can attain about 90% with 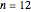 . The computation of power in the one-sample t-test is discussed in many textbooks (see also Noncentral t-distribution). To exit the power curve display, uncheck the checkbox.
. The computation of power in the one-sample t-test is discussed in many textbooks (see also Noncentral t-distribution). To exit the power curve display, uncheck the checkbox.
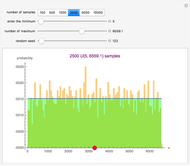
Snapshot 7: When 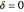 is selected, we can explore how the t-test behaves when the null hypothesis is true. In this case the
is selected, we can explore how the t-test behaves when the null hypothesis is true. In this case the 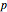 -value is uniformly distributed between 0 and 1. When the "random seed" slider is changed, fresh
-value is uniformly distributed between 0 and 1. When the "random seed" slider is changed, fresh 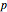 -values and confidence intervals are generated. If
-values and confidence intervals are generated. If  is increased, the
is increased, the 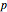 -values are still random but tend to be smaller reflecting the fact that
-values are still random but tend to be smaller reflecting the fact that 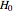 becomes less tenable.
becomes less tenable.
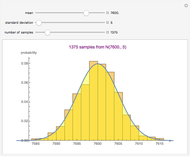
Snapshot 8: Similar to snapshot 7, but we just show the true distribution and the sampling distribution and ignore the hypothesis testing.
Many other scenarios that offer illuminating insights may be obtained by experimenting with other settings.
Reference
[1] G. van Belle, Statistical Rules of Thumb, 2nd ed., New York: Wiley, 2008.
Permanent Citation