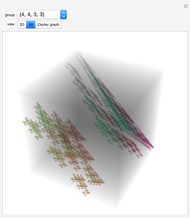
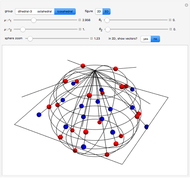
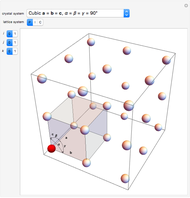
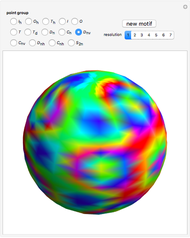
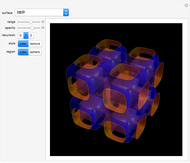
A crystallographic point group has a set of symmetry operations including rotations, reflections, and inversions (whose total number determines the order of the group), restricted by compatibility with translational symmetry. There are 32 such groups, enumerated by the control "i". This Demonstration shows their multiplication tables and Cayley graphs. Each element of the group is enumerated and, because the products again belong to the same set, they first appear colored as a usual 2D array with colors depending on the enumeration scheme. 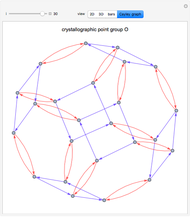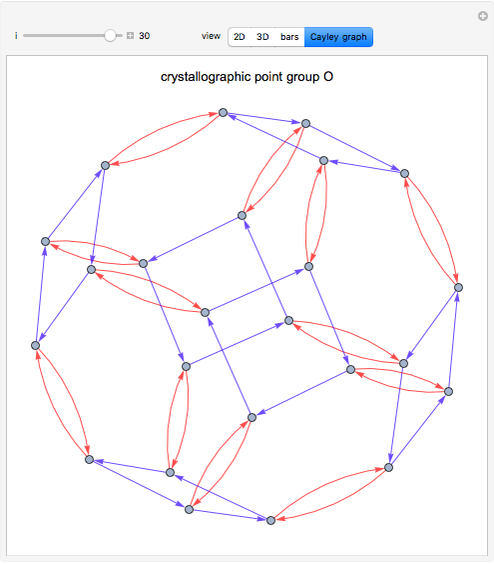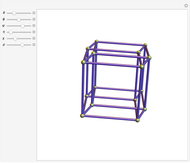Afterward, in 3D plots, these values are interpreted as a height for each product , first with cuboids and afterward with columns. (A Cayley graph encodes how the products of the group generators produce all the elements of the group [mouseover the vertices]). The graphs include the identity and the generators can be chosen, modifying the resulting graph. The vertices of the graph represent the elements of the group and the directed edges generators; then the edge that connects an element with others represents that the product of the first element with the generator gives the second, codified as permutation cycles. Mouseover the graphics to see the crystal system to which each group belongs (cubic, tetragonal, orthorhombic, monoclinic, triclinic, trigonal, hexagonal) and the elements of the group.