Curvature and Torsion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
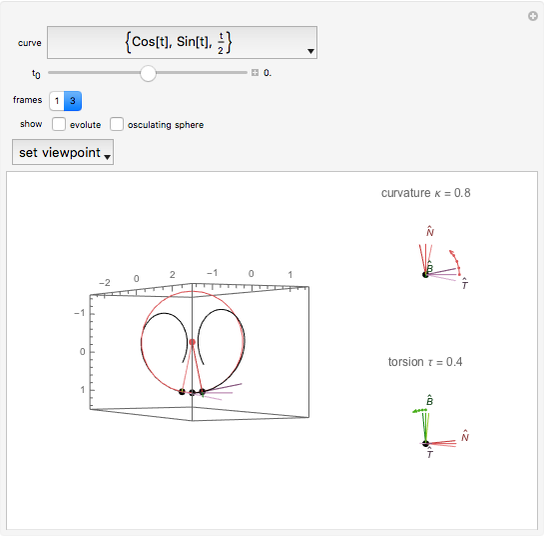
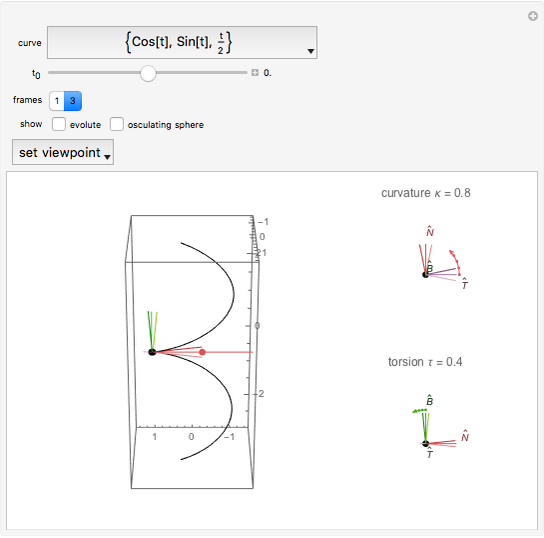
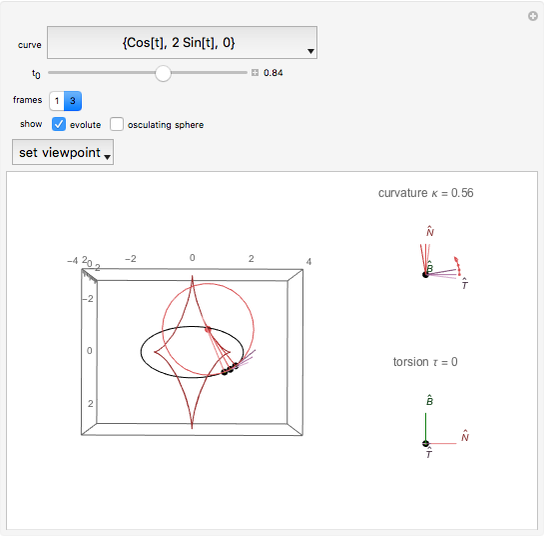
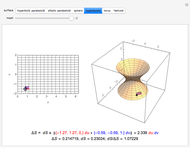
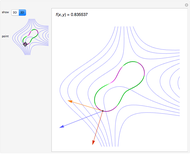
Choose among several curves and see the rotation of the Frenet–Serret frame as you move the slider. From this you can perceive the curvature and torsion of the curve. Associated objects (such as the circle of curvature, evolute, and osculating sphere, as well as two views of the Frenet frames) may be displayed.
Contributed by: Michael Rogers (Oxford College/Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
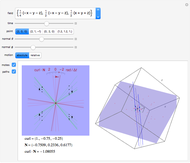
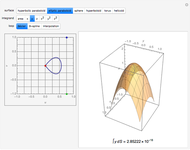
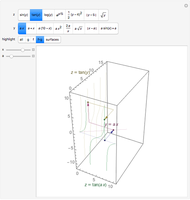
Select a curve from the top drop-down menu (a description is given in the menu, but the equation will be displayed on the button). Move the  slider to move the point along the curve. The frames, circle of curvature, etc. will move with it. You may select just one frame at
slider to move the point along the curve. The frames, circle of curvature, etc. will move with it. You may select just one frame at  , or three, which includes one before and one after
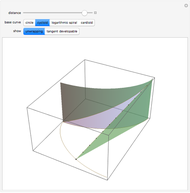
, or three, which includes one before and one after  . You may choose to display the evolute and the osculating sphere. The "set viewpoint" menu sets the viewpoint to show either the curvature or torsion, if defined. For curvature, the viewpoint is down along the binormal; for torsion it is into the tangent.
. You may choose to display the evolute and the osculating sphere. The "set viewpoint" menu sets the viewpoint to show either the curvature or torsion, if defined. For curvature, the viewpoint is down along the binormal; for torsion it is into the tangent.
The curvature is the angular rate (radians per unit arc length) at which the tangent vector turns about the binormal vector (that is, 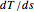 ). It is represented here in the top-right graphic by an arc equal to the product of it and one unit of arc length. The torsion is the angular rate at which the binormal vector turns about the tangent vector (that is,
). It is represented here in the top-right graphic by an arc equal to the product of it and one unit of arc length. The torsion is the angular rate at which the binormal vector turns about the tangent vector (that is, 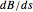 ). It is represented in the bottom-right graphic also by an arc equal to it times a unit. The evolute is the curve traced by the center of curvature.
). It is represented in the bottom-right graphic also by an arc equal to it times a unit. The evolute is the curve traced by the center of curvature.
Snapshot 1: helix, curvature view
Snapshot 2: helix, torsion view
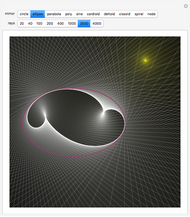
Snapshot 3: ellipse, with evolute
Permanent Citation